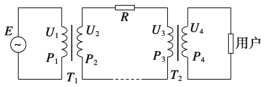
题目内容
【题目】如图所示，C是放在光滑的水平面上的一块木板，木板的质量为3m，在木板的上面有两块质量均为m的小木块A和B，它们与木板间的动摩擦因数均为μ．最初木板静止，A、B两木块同时以方向水平向右的初速度v0和2v0在木板上滑动，木板足够长，A、B始终未滑离木板．求：
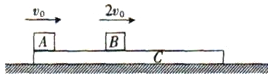
（1）木块B从刚开始运动到与木板C速度刚好相等的过程中，木块B所发生的位移；
（2）木块A在整个过程中的最小速度；
（3）整个过程中，A、B两木块相对于滑板滑动的总路程是多少？
【答案】（1）
，（2）
，（3）
【解析】
试题分析：（1）木块A先做匀减速直线运动，后做匀加速直线运动；木块B一直做匀减速直线运动；木板C做两段加速度不同的匀加速直线运动，直到A、B、C三者的速度相等为止，设为v1．对A、B、C三者组成的系统，由动量守恒定律得：mv0+2mv0=（m+m+3m）v1
解得：v1=0．6 v0
对木块B运用动能定理，有：
解得：
（2）设木块A在整个过程中的最小速度为v′，所用时间为t，由牛顿第二定律：
对木块A：a1=μmg/m=μg，对木块C：a2=2μmg/3m=2μg/3，
当木块A与木板C的速度相等时，木块A的速度最小，因此有：v0-μgt=（2μg/3）t
解得t=3v0/（5μg）
木块A在整个过程中的最小速度为：v′=v0-a1t=2v0 /5．
（3）Q总=Q1+Q2 = fs相1+fs相2=ΔEk损
所以
练习册系列答案
相关题目
