题目内容
7.假设地球可视为质量均匀分布的球体.已知地球表面重力加速度在两极的大小为g0;在赤道的大小为g;地球自转的周期为T;引力常量为G.则( )| A. | 地球的半径R=$\frac{{{(g}_{0}-g)T}^{2}}{4{π}^{2}}$ | |
| B. | 地球的半径R=$\frac{{{g}_{0}T}^{2}}{{4π}^{2}}$ | |
| C. | 地球的第一宇宙速度为$\frac{T}{2π}\sqrt{{g}_{0}{(g}_{0}-g)}$ | |
| D. | 地球的第一宇宙速度为 $\frac{T}{2π\sqrt{g{(g}_{0}-g)}}$ |
分析 质量为m的物体在两极所受地球的引力等于其所受的重力.根据万有引力定律和牛顿第二定律,在赤道的物体所受地球的引力等于其在两极所受的重力联立求半径,再由第一宇宙速度为v=$\sqrt{\frac{GM}{R}}$,即可求解.
解答 解:AB、在两极地区,物体受到地球的万有引力,其大小为mg0,在赤道处,地球对物体的万有引力大小仍为mg0,
万有引力和重力的合力提供圆周运动向心力有即有:
m(g0-g)=m$\frac{4{π}^{2}R}{{T}^{2}}$
解得:R=$\frac{({g}_{0}-g){T}^{2}}{4{π}^{2}}$,故A正确,B错误;
CD、质量为m的物体在两极所受地球的引力等于其所受的重力,有:$\frac{GMm}{{R}^{2}}$=mg0,
解得:M=$\frac{{g}_{0}({g}_{0}-g)^{2}{T}^{4}}{16{π}^{4}G}$
那么地球的第一宇宙速度为v=$\sqrt{\frac{GM}{R}}$=$\frac{T}{2π}\sqrt{{g}_{0}{(g}_{0}-g)}$,故C正确,D错误;
故选:AC.
点评 解决本题的关键是认识到在赤道处的重力实为地球对物体的万有引力减去物体随地球自转的向心力,掌握力的关系是正确解题的前提.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.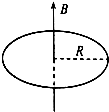 用粗细确定的金属丝制成N匝圆形闭合线圈,半径为R,垂直放在匀强磁场中,如图所示,当磁场的磁感应强度随时间均匀增大时,下列说法中正确的是( )
用粗细确定的金属丝制成N匝圆形闭合线圈,半径为R,垂直放在匀强磁场中,如图所示,当磁场的磁感应强度随时间均匀增大时,下列说法中正确的是( )
 用粗细确定的金属丝制成N匝圆形闭合线圈,半径为R,垂直放在匀强磁场中,如图所示,当磁场的磁感应强度随时间均匀增大时,下列说法中正确的是( )
用粗细确定的金属丝制成N匝圆形闭合线圈,半径为R,垂直放在匀强磁场中,如图所示,当磁场的磁感应强度随时间均匀增大时,下列说法中正确的是( )| A. | 线圈中产生的感应电动势E与半径R成正比 | |
| B. | 线圈中产生的感应电流I与半径R成正比 | |
| C. | 线圈中产生的感应电动势E与匝数N成正比 | |
| D. | 线圈中产生的感应电流I与匝数N成正比 |
17.关于自由落体运动的理解,下列说法正确的是( )
| A. | 加速度为g的匀变速直线运动是自由落体运动 | |
| B. | 初速度为零且竖直向下的运动是自由落体 | |
| C. | 只在重力作用下且竖直向下的运动是自由落体运动 | |
| D. | 自由落体运动在任一相等的时间内速度变化量相等 |
 如图所示,矩形线框在竖直平面内从静止开始下落,若线框在进入磁场过程中速度增大,则在该过程中线框下落的加速度减小.(填“增大”、“减小”或“不变”)
如图所示,矩形线框在竖直平面内从静止开始下落,若线框在进入磁场过程中速度增大,则在该过程中线框下落的加速度减小.(填“增大”、“减小”或“不变”)
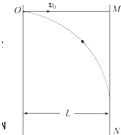 某同学做了以下实验来探究平抛运动的规律,从O点以初速度v0水平抛出一小球,在距抛出点L处竖直放置一光屏MN,如图所示,离小球抛出点很近处有一很小的光源,使小球的影子投射在屏上,试分析:当小球做平抛运动时,小球在光屏MN上的影子将做何运动?
某同学做了以下实验来探究平抛运动的规律,从O点以初速度v0水平抛出一小球,在距抛出点L处竖直放置一光屏MN,如图所示,离小球抛出点很近处有一很小的光源,使小球的影子投射在屏上,试分析:当小球做平抛运动时,小球在光屏MN上的影子将做何运动?