题目内容
2.N匝边长为L的正方形线圈与匀强磁场B垂直,线圈总电阻为R,当线圈绕其对称轴在磁场中转过60°时,通过导线任一截面的电量为$\frac{NB{L}^{2}}{2R}$.分析 由法拉第电磁感应定律求出感应电动势,由欧姆定律求出电流,由电流定义式求出电荷量,从而即可求解.
解答 解:线圈转过60°的过程中感应电动势的平均值$\overline{E}$=N$\frac{△∅}{△t}$=N$\frac{B{L}^{2}}{\frac{π}{3ω}}$cos60°=$\frac{3NB{L}^{2}ω}{2π}$.
感应电流的平均值$\overline{I}$=$\frac{\overline{E}}{R}$=$\frac{3NB{L}^{2}ω}{2πR}$.
通过导线截面电量q=$\overline{I}$△t=$\frac{3NB{L}^{2}ω}{2πR}$•$\frac{π}{3ω}$=$\frac{NB{L}^{2}}{2R}$
故答案为:$\frac{NB{L}^{2}}{2R}$.
点评 本题考查了导线任一截面的电荷量,应用法拉第电磁感应定律、欧姆定律、电流定义式,并注意感应电动势的平均值与瞬时值的区别.

练习册系列答案
相关题目
13.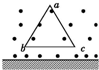 如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )
如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )
 如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )
如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )| A. | 铝框回路中的磁通量变大,有顺时针方向的感应电流产生 | |
| B. | 回路中的感应电流沿顺时针方向,底边bc两端间的电势差为0 | |
| C. | 铝框下落的加速度大小一定小于重力加速度g | |
| D. | 底边bc受到的安培力向上,折线bac受到的安培力向下,铝框下落时的加速度大小可能等于g |
17.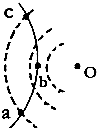 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
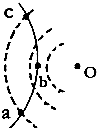 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )| A. | 此粒子一直受到静电吸引力作用 | |
| B. | 粒子在b点的电势能一定大于在a点的电势能 | |
| C. | 粒子在a 点和c点的速度相同 | |
| D. | 粒子在b 点的速度一定大于在a 点的速度 |
7.假设地球可视为质量均匀分布的球体.已知地球表面重力加速度在两极的大小为g0;在赤道的大小为g;地球自转的周期为T;引力常量为G.则( )
| A. | 地球的半径R=$\frac{{{(g}_{0}-g)T}^{2}}{4{π}^{2}}$ | |
| B. | 地球的半径R=$\frac{{{g}_{0}T}^{2}}{{4π}^{2}}$ | |
| C. | 地球的第一宇宙速度为$\frac{T}{2π}\sqrt{{g}_{0}{(g}_{0}-g)}$ | |
| D. | 地球的第一宇宙速度为 $\frac{T}{2π\sqrt{g{(g}_{0}-g)}}$ |
14.关于斜抛运动的性质以下说法正确的是( )
| A. | 斜抛运动是匀变速运动,因为其速度是恒定的 | |
| B. | 斜抛运动是匀变速运动,因为其加速度是恒定的 | |
| C. | 斜抛运动是非匀变速运动,因为其速度是变化的 | |
| D. | 斜抛运动是非匀变速运动,因为其加速度是变化的 |
12.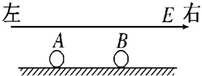 如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )
如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )
 如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )
如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )| A. | 小球 A带正电,小球 B带负电,且 QA>QB | |
| B. | 小球 A带正电,小球 B带负电,且 QA<QB | |
| C. | 小球 A带负电,小球 B带正电,且 QA>QB | |
| D. | 小球 A带负电,小球 B带正电,且 QA<QB |
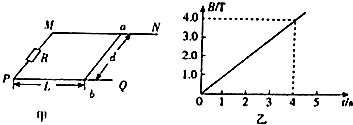 如图甲所示,两根足够长的粗糙平行金属导轨MN、PQ固定在同一绝缘水平面上,两导轨间距为d=1m,导轨电阻忽略不计,M、P间连接一阻值R=1.5Ω的电阻.现有一质量为m=0.4kg,阻值r=0.5Ω的金属棒ab垂直于导轨放在两导轨上并与导轨接触良好,金属棒与电阻R间的距离为L=4m,整个装置处于一竖直方向的匀强磁场中,磁感应强度大小随时间变化的情况如图乙所示,已知金属棒与导轨间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,求:
如图甲所示,两根足够长的粗糙平行金属导轨MN、PQ固定在同一绝缘水平面上,两导轨间距为d=1m,导轨电阻忽略不计,M、P间连接一阻值R=1.5Ω的电阻.现有一质量为m=0.4kg,阻值r=0.5Ω的金属棒ab垂直于导轨放在两导轨上并与导轨接触良好,金属棒与电阻R间的距离为L=4m,整个装置处于一竖直方向的匀强磁场中,磁感应强度大小随时间变化的情况如图乙所示,已知金属棒与导轨间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,求: