题目内容
16.如图为接在50Hz低压交流电源上的打点计时器,在纸带做匀加速直线运动时打出的一条纸带,图中所示的是每打5个点所取的记数点,但第3个记数点没有画出.由图数据可求得(结果均保留2位有效数字):
(1)该物体的加速度为2.0m/s2,
(2)第3个记数点与第2个记数点的距离约为4.83cm,
(3)打第3个点时该物体的速度约为0.583m/s.
分析 物体做的是匀变速直线运动,(1)求解加速度时首先想到的应该是逐差法,但是只有两组数据,所以要找两组数据之间的关系,推论xm-xn=(m-n)at2可提供这两组数据与加速度的关系,应用这个推论即可.
(2)第2、3两点间的距离对应的应该为x2,要想得到x2必须找他和已知量的关系,x2-x1=at2提供了这个关系.
(3)为了让结果更精确,我们需要用上这两组数据,而这两组数据只能求他们自己这段位移中的平均速度,v3需要找它与这两个平均速度的关系:而v3对应的时刻为这两个速度所对应的时间的中间时刻,可由${v}_{\frac{t}{2}}$=$\frac{{v}_{0}+v}{2}$求出.
解答 解:(1)设Ab间的位移为x1,BC间的位移为x2,CD间的位移为x3,DE间的位移为x4;
因为周期为T=0.02s,且每打5个点取一个记数点,所以每两个点之间的时间间隔T=0.1s;
由匀变速直线运动的推论xm-xn=(m-n)at2得:
x4-x1=3at2带入数据得:
(8.83-2.83)×10-2=3a×0.12
解得:a=2.0m/s2.
(2)第3个记数点与第2个记数点的距离即为x2,由匀变速直线运动的推论:x2-x1=aT2得:
x2=x1+aT2带入数据得:
x2=2.83×10-2+2.0×0.12=0.0483m=4.83cm
(3)为了让结果更精确,我们需要用上这两组数据:设AB两点间中间时刻的速度为v1,DE点间的中间时刻的速度速度为v2
则:v1=$\frac{{x}_{1}}{T}$,v2=$\frac{{x}_{4}}{T}$带入数据得:
得:v1=0.283m/s,v2=0.883m/s
因为点3为v1v2所对应的时间的中间时刻,所以由${v}_{\frac{t}{2}}$=$\frac{{v}_{0}+v}{2}$得:
v3=$\frac{{v}_{1}+{v}_{2}}{2}$,带入数据得:
v3=$\frac{0.283+0.883}{2}m/s=0.583m/s$
故答案为:(1)2.0; (2)4.83; (3)0.583
点评 匀变速直线运动的推论,无论是实验还是平时计算上用处很多需要熟练掌握.处理实验数据时还应该注意单位换算和有效数字的保留.

| A. | 2I | B. | 3I | C. | $\sqrt{3}$I | D. | 无法确定 |
| A. | 地球的半径R=$\frac{{{(g}_{0}-g)T}^{2}}{4{π}^{2}}$ | |
| B. | 地球的半径R=$\frac{{{g}_{0}T}^{2}}{{4π}^{2}}$ | |
| C. | 地球的第一宇宙速度为$\frac{T}{2π}\sqrt{{g}_{0}{(g}_{0}-g)}$ | |
| D. | 地球的第一宇宙速度为 $\frac{T}{2π\sqrt{g{(g}_{0}-g)}}$ |
 如图所示是一个由电池、电阻R与平行板电容器组成的串联电路,在增大电容器两极板距离的过程中,下列说法正确的是( )
如图所示是一个由电池、电阻R与平行板电容器组成的串联电路,在增大电容器两极板距离的过程中,下列说法正确的是( )| A. | 电阻R中没有电流 | B. | 电容器的电容变小 | ||
| C. | 电阻R中有从a流向b的电流 | D. | 电阻R中有从b流向a的电流 |
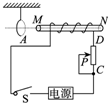 如图所示装置中,闭合铜环A静止悬挂在通电螺线管的M端,螺线管的轴线垂直于环面并正对环心.要使铜环向螺线管靠近,下列各操作中可以实现的是( )
如图所示装置中,闭合铜环A静止悬挂在通电螺线管的M端,螺线管的轴线垂直于环面并正对环心.要使铜环向螺线管靠近,下列各操作中可以实现的是( )| A. | 开关S由断开到接通的瞬间 | B. | 开关S由接通到断开的瞬间 | ||
| C. | 将滑片P向C滑动的过程中 | D. | 将滑片P向D滑动的过程中 |
 地球大气层外部有一层复杂的电离层,既分布有地磁场,又分布有电场.假设某时刻在该空间中有一小区域存在如图所示的电场和磁场;电场的方向在纸面内斜向左下方,磁场的方向垂直于纸面向里.此时一带电粒子恰以速度v垂直于电场和磁场射入该区域,不计重力作用,则在该区域中,有关该带电粒子的运动情况可能的是( )
地球大气层外部有一层复杂的电离层,既分布有地磁场,又分布有电场.假设某时刻在该空间中有一小区域存在如图所示的电场和磁场;电场的方向在纸面内斜向左下方,磁场的方向垂直于纸面向里.此时一带电粒子恰以速度v垂直于电场和磁场射入该区域,不计重力作用,则在该区域中,有关该带电粒子的运动情况可能的是( )| A. | 仍做直线运动 | B. | 立即向左下方偏转 | ||
| C. | 做匀变速直线运动 | D. | 可能做匀速圆周运动 |
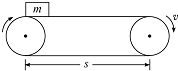 如图所示,水平传送带的速度v=3m/s,两轮的圆心距离s=4.5m,现将m=1kg的小物体轻放到左轮正上方的传送带上,物体与传送带间的动摩擦因数为μ=0.15,电动机带动传送带将物体从左轮运送到右轮正上方时,电动机消耗的电能是多少?
如图所示,水平传送带的速度v=3m/s,两轮的圆心距离s=4.5m,现将m=1kg的小物体轻放到左轮正上方的传送带上,物体与传送带间的动摩擦因数为μ=0.15,电动机带动传送带将物体从左轮运送到右轮正上方时,电动机消耗的电能是多少?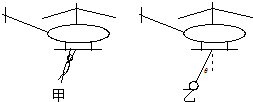
 如图所示,光滑的斜面体质量为M,倾角为θ,长为L,质量为m小物块从斜面体顶端由静止开始下滑,斜面位于光滑的水平地面上.从地面上看,在小物块沿斜面下滑的过程中,斜面体运动的位移?
如图所示,光滑的斜面体质量为M,倾角为θ,长为L,质量为m小物块从斜面体顶端由静止开始下滑,斜面位于光滑的水平地面上.从地面上看,在小物块沿斜面下滑的过程中,斜面体运动的位移?