题目内容
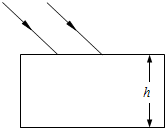
如图所示，某三棱镜的截面是一直角三角形，棱镜材料的折射率为n，底面BC涂黑，入射光沿平行于底面BC的方向射向AB而，经AB和AC折射后射出．为了使上述入射光线能从AC面射出，求折射率n的取值范围．
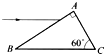
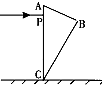
画出光路图如图所示．
因为入射光平行于BC面，i=60°
由折射定律有
=n，解得sinα=
光折到AC面上时，
=n
由几何关系可得：α+β=90°
则sinβ=cosα=
=
sinr=nsinβ=
要使有光线从AC面射出，应有sinr≤1：即
≤1
解得n≤
．
答：折射率n的取值范围1＜n≤
．
因为入射光平行于BC面，i=60°
由折射定律有
| sini |
| sinα |
| ||
| 2n |
光折到AC面上时，
| sinr |
| sinβ |
由几何关系可得：α+β=90°
则sinβ=cosα=
| 1-sin2α |
| ||
| 2n |
sinr=nsinβ=
| ||
| 2 |
要使有光线从AC面射出，应有sinr≤1：即
| ||
| 2 |
解得n≤
| ||
| 2 |
答：折射率n的取值范围1＜n≤
| ||
| 2 |
练习册系列答案
孟建平名校考卷系列答案
相关题目
