题目内容
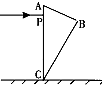
如图所示,ABC为一块立在水平地面上的玻璃砖的截面示意图,△ABC为一直角三角形,∠ABC=90°,∠BAC=60°,AB边长度为L=12m,AC垂直于地面放置.现在有一束单色光垂直于AC边从P点射入玻璃砖,折射率n=
,已知PA=
L,该束光最终射到了水平地面上某点,试求该点距离C点的距离.(取tan15°≈0.25)
| 2 |
| 1 |
| 8 |

由题意知,设临界角为C,则有n=
,可得:C=45°
由几何知识得:当单色光照射到AB上时入射角为i=60°>C,将发生全反射,入射点为R,然后射入到BC面上Q点,入射角为i′=30°,取折射角为θ,根据折射定律有:
=n
可得:θ=45°
最终单色光射到地面上的K点,如图有:
AR=
=
×12m=3m,BQ=(AB-AR)tan30°=(12-3)×
m=3
m,
则CQ=BC-BQ=12
m-3
m=9
m,
由此可知:CS=CQcos60°=
m,SK=CQsin60°tan15°=
×
×(2-
)≈1.8m
所以入射点距离C点:d=SK+CS=(1.8+
)m≈9.5m
答:该点距离C点的距离约为9.5m.

| 1 |
| sinC |
由几何知识得:当单色光照射到AB上时入射角为i=60°>C,将发生全反射,入射点为R,然后射入到BC面上Q点,入射角为i′=30°,取折射角为θ,根据折射定律有:
| sinθ |
| sin30° |
可得:θ=45°
最终单色光射到地面上的K点,如图有:
AR=
| ||
| sin30° |
| 1 |
| 4 |
| ||
| 3 |
| 3 |
则CQ=BC-BQ=12
| 3 |
| 3 |
| 3 |
由此可知:CS=CQcos60°=
9
| ||
| 2 |
9
| ||
| 2 |
| ||
| 2 |
| 3 |
所以入射点距离C点:d=SK+CS=(1.8+
9
| ||
| 2 |
答:该点距离C点的距离约为9.5m.


练习册系列答案
相关题目
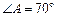 ,入射光线垂直于AB面,求光线从棱镜第一次折射射入空气时的折射角,并作出光路图,已知折射率
,入射光线垂直于AB面,求光线从棱镜第一次折射射入空气时的折射角,并作出光路图,已知折射率