Question

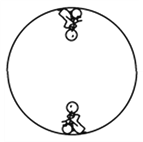
【题目】如图，杂技节目飞车表演时，一摩托车在竖直的圆轨道内侧做匀速圆周运动，人和车的总质量为m，轨道半径为R，车经最高点时发动机功率为P0、车对轨道的压力为mg。设轨道对摩托车的阻力与车对轨道的压力成正比，则

A. 车经最低点时对轨道的压力为3mg

B. 车运动过程中发动机的功率一直不变

C. 车经最低点时发动机功率为3P0

D. 车从最高点经半圆轨道到最低点的过程中，人和车重力做功的功率不变

Answer 1

【答案】AC

【解析】A：在最高点时，对人和车整体受力分析，由牛顿第二定律可得：

在最低点时，对人和车整体受力分析，由牛顿第二定律可得：

联立解得： ，据牛顿第三定律可得：车经最低点时对轨道的压力为3mg。故A项正确。

B：车运动过程中，车对轨道的压力变化，轨道对摩托车的阻力与车对轨道的压力成正比，轨道对摩托车的阻力变化，摩托车在竖直的圆轨道内侧做匀速圆周运动，牵引力等于阻力，则车运动过程中发动机的功率变化。故B项错误。

C：由A项解析可知，车经最低点时对轨道压力是车经最高点时对轨道压力的3倍，轨道对摩托车的阻力与车对轨道的压力成正比，摩托车在竖直的圆轨道内侧做匀速圆周运动，牵引力等于阻力，所以车经最低点时牵引力力是车经最高点时牵引力的3倍；发动机的功率，车经最低点时发动机功率是车经最高点时发动机功率的3倍。故C项正确。

D：车匀速从最高点经半圆轨道到最低点的过程中，竖直方向的分速度不断变化，人和车重力做功的功率不断变化。故D项错误。