��Ŀ����
����Ŀ����ͼ��ʾ���㹻����ƽ�й⻬����̶���ˮƽ���ϣ�������ΪL=1m�����Ҷ������ж�ֵ����R=2��������װ�ô��ڴ�ֱ����ƽ��Ÿ�Ӧǿ��B=1T����ǿ�ų��У�һ����m=2kg�Ľ������ں㶨��ˮƽ����F=10N�������£��ڵ������ɾ�ֹ��ʼ�����˶����˶��н�����ʼ���뵼�촹ֱ�����켰�������ĵ��費�ƣ�����˵����ȷ���ǣ� ��
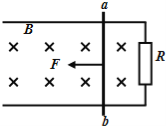
A�������ĸ�Ӧ���������ڽ���������aָ��b
B���������������ȼ��ٺ�����˶�ֱ����ֹ
C���������������ٶ�Ϊ5m/s2
D��ˮƽ�����������Ϊ200W
���𰸡�ACD
��������
��������������ֶ����жϸ�Ӧ�����ķ��������������Ͱ������������˶���ͨ�������������ı仯���жϼ��ٶȵı仯������ȷ�������ٶȣ����������ڰ�����ʱ���ٶȴﵽ�����и�����ĸ�Ӧ�綯�ƹ�ʽ���պϵ�·ŷķ�����Լ���������С��ʽ�������ٶȵĴ�С����P=Fv�������������ʣ�
�⣺A�������������˶��и�Ÿ��ߣ��������ֶ����жϵ�֪�����ĸ�Ӧ����������a��b����A��ȷ��
B�����������ܵİ�������С�����������������˶������������������ֱ���˶����ٶȴﵽ���B����
C������ţ�ٵڶ����ɵã�F��![]() =ma����֪�������ٶ�v�����ٶ�a��С�������տ�ʼ�˶�ʱ���ٶ���������ٶ�Ϊ��am=
=ma����֪�������ٶ�v�����ٶ�a��С�������տ�ʼ�˶�ʱ���ٶ���������ٶ�Ϊ��am=![]() =
=![]() =5m/s2����C��ȷ��
=5m/s2����C��ȷ��
D�����������ٶ�Ϊvm����ʱa=0�����У�F=![]() ���ã�vm=
���ã�vm=![]() =
=![]() m/s=20m/s
m/s=20m/s
����ˮƽ�����������Ϊ��Pm=Fvm=10��20W=200W����D��ȷ��
��ѡ��ACD��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�