题目内容
1. 如图所示,水平地面上有一个坑,其竖直截面为半圆,ab为沿水平方向的直径.若在A点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,重力加速度为g,求圆的半径.
如图所示,水平地面上有一个坑,其竖直截面为半圆,ab为沿水平方向的直径.若在A点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,重力加速度为g,求圆的半径.
分析 根据几何关系求出小球平抛运动的水平位移和竖直位移,结合平抛运动的规律求出圆的半径.
解答  解:如图所示,h=$\frac{R}{2}$,则Od=$\frac{\sqrt{3}}{2}R$,
解:如图所示,h=$\frac{R}{2}$,则Od=$\frac{\sqrt{3}}{2}R$,
小球做平抛运动的水平位移x=R+$\frac{\sqrt{3}}{2}R$
竖直位移y=h=$\frac{R}{2}$,
根据y=$\frac{1}{2}g{t}^{2}$,x=v0t
联立以上两式解得R=$\frac{4{{v}_{0}}^{2}}{(7+4\sqrt{3})g}$.
答:圆的半径为$\frac{4{{v}_{0}}^{2}}{(7+4\sqrt{3})g}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
11. 如图所示,电路中,A、B是两个完全相同的灯泡,L是一个理想电感线圈(线圈直流电阻不计),C是电容相当大的电容器,当S闭合与断开时,A、B的亮度情况正确的是( )
如图所示,电路中,A、B是两个完全相同的灯泡,L是一个理想电感线圈(线圈直流电阻不计),C是电容相当大的电容器,当S闭合与断开时,A、B的亮度情况正确的是( )
 如图所示,电路中,A、B是两个完全相同的灯泡,L是一个理想电感线圈(线圈直流电阻不计),C是电容相当大的电容器,当S闭合与断开时,A、B的亮度情况正确的是( )
如图所示,电路中,A、B是两个完全相同的灯泡,L是一个理想电感线圈(线圈直流电阻不计),C是电容相当大的电容器,当S闭合与断开时,A、B的亮度情况正确的是( )| A. | S闭合时,A灯亮,然后逐渐熄灭 | |
| B. | S闭合时,B立即亮,然后逐渐熄灭 | |
| C. | S闭合足够长时间后,B发光,而A不发光 | |
| D. | S闭合足够长时间后再断开,B立即熄灭,而A逐渐熄灭 |
12. 在反恐演习中,中国特种兵进行了飞行跳伞表演.某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵速度随时间变化的规律如图所示.下列结论正确的是( )
在反恐演习中,中国特种兵进行了飞行跳伞表演.某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵速度随时间变化的规律如图所示.下列结论正确的是( )
 在反恐演习中,中国特种兵进行了飞行跳伞表演.某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵速度随时间变化的规律如图所示.下列结论正确的是( )
在反恐演习中,中国特种兵进行了飞行跳伞表演.某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵速度随时间变化的规律如图所示.下列结论正确的是( )| A. | 在t0~3t0的时间内,平均速度$\overline{v}$>$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| B. | 降落伞打开后,降落伞和伞兵所受的阻力越来越大 | |
| C. | 在0~t0时间内加速度不变,在t0~3t0时间内加速度变大 | |
| D. | 若第一个伞兵在空中打开降落伞时第二个伞兵立即跳下,则他们在空中的距离先增大后减小 |
6. 如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )
如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )
 如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )
如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )| A. | 有顺时针方向的感应电流 | B. | 有逆时针方向的感应电流 | ||
| C. | 先逆时针后顺时针方向的感应电流 | D. | 无感应电流 |
13.一质点做简谐运动的图象如图所示,下列说法正确的是( )


| A. | 0~1s速度在增大 | B. | 0~1s位移在增大 | ||
| C. | 2~3s加速度在增大 | D. | 2~3s位移在增大 |
10.“研究平抛物体的运动”实验的装置如图所示,下列实验要求正确的是( )
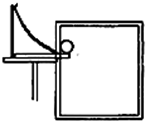

| A. | 将斜槽的末端切线调成水平 | |
| B. | 斜槽轨道必须是光滑的 | |
| C. | 小球每次必须从斜面上的同一位置由静止开始释放 | |
| D. | 在白纸上记录斜槽末端槽口的位置O,作为小球做平抛运动的起点和所建坐标系的原点 |
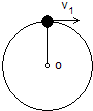 长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求:
长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求: