题目内容
8.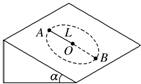 如图所示,在倾角为α=30°的光滑斜面上,有一根长为L=0.8m的细绳,一端固定在O点,另一端系一质量为m=0.2kg的小球,小球沿斜面做圆周运动,若要小球能通过最高点A,g取10m/s2,则小球在最低点B的最小速度是( )
如图所示,在倾角为α=30°的光滑斜面上,有一根长为L=0.8m的细绳,一端固定在O点,另一端系一质量为m=0.2kg的小球,小球沿斜面做圆周运动,若要小球能通过最高点A,g取10m/s2,则小球在最低点B的最小速度是( )| A. | 2 m/s | B. | 2$\sqrt{6}$m/s | C. | 2$\sqrt{5}$ m/s | D. | 2$\sqrt{2}$ m/s |
分析 小球恰好能在斜面上做完整的圆周运动,说明小球在A点时细线的拉力为零,只有重力的分力做向心力.
从A到B的过程中只有重力做功,由机械能守恒定律可以求得B点时的速度.
解答 解:小球恰好能在斜面上做完整的圆周运动,刚小球通过A点时细线的拉力为零,根据圆周运动和牛顿第二定律有:
mgsinα=$m\frac{{{v}_{A}}^{2}}{L}$
小球通过最高点的最小速度为:vA=$\sqrt{gLsinα}$=2 m/s,
在B点的最小速度vB满足:$\frac{1}{2}$mvB2=$\frac{1}{2}$mvA2+2mgLsin α,
解得:vB=2$\sqrt{5}$ m/s,故C正确.
故选:C
点评 要了解物体做圆周运动的特点,同时也用到机械能守恒,是一个很好的综合题目,很能考查学生的分析解题能力.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
19.物体沿光滑斜面向下加速滑动,在运动过程中,下述说法正确的是( )
| A. | 重力势能逐渐减少,动能也逐渐减少 | |
| B. | 重力势能逐渐增加,动能逐渐减少 | |
| C. | 物体在运动过程中,机械能一定守恒 | |
| D. | 重力和支持力对物体都做正功 |
16.2014年APEC领导人非正式会议于11月10日到11日在北京召开,期间在奥林匹克中心举行了盛大的主题为“自然颂”的烟火表演,按照设计要求,装有焰火的礼花弹从专用炮筒射出后,在5s末达到离地面200m的最高点,随即炸开.构成各种美丽的花卉、鸟类图案,假设礼花弹从炮筒中射出时的初速度时v0,上升过程中所受的平均阻力大小始终是自身重力的k倍,那么v0和k分别等于( )
| A. | 60m/s,0.6 | B. | 80m/s,0.6 | C. | 60m/s,1.6 | D. | 80m/s,1.6 |
3. “神舟十号”与“天宫一号”已5次成功实现交会对接.如图所示,交会对接前“神舟十号”飞船先在较低圆轨道1上运动,在适当位置经变轨与在圆轨道2上运动的“天宫一号”对接.M、Q两点在轨道1上,P点在轨道2上,三点连线过地球球心,把飞船的加速过程简化为只做一次短时加速.下列关于“神舟十号”变轨过程的描述,正确的有( )
“神舟十号”与“天宫一号”已5次成功实现交会对接.如图所示,交会对接前“神舟十号”飞船先在较低圆轨道1上运动,在适当位置经变轨与在圆轨道2上运动的“天宫一号”对接.M、Q两点在轨道1上,P点在轨道2上,三点连线过地球球心,把飞船的加速过程简化为只做一次短时加速.下列关于“神舟十号”变轨过程的描述,正确的有( )
 “神舟十号”与“天宫一号”已5次成功实现交会对接.如图所示,交会对接前“神舟十号”飞船先在较低圆轨道1上运动,在适当位置经变轨与在圆轨道2上运动的“天宫一号”对接.M、Q两点在轨道1上,P点在轨道2上,三点连线过地球球心,把飞船的加速过程简化为只做一次短时加速.下列关于“神舟十号”变轨过程的描述,正确的有( )
“神舟十号”与“天宫一号”已5次成功实现交会对接.如图所示,交会对接前“神舟十号”飞船先在较低圆轨道1上运动,在适当位置经变轨与在圆轨道2上运动的“天宫一号”对接.M、Q两点在轨道1上,P点在轨道2上,三点连线过地球球心,把飞船的加速过程简化为只做一次短时加速.下列关于“神舟十号”变轨过程的描述,正确的有( )| A. | “神舟十号”在M点加速,可以在P点与“天宫一号”相遇 | |
| B. | “神舟十号”在M点经一次加速,即可变轨到轨道2 | |
| C. | “神舟十号”经变轨后速度总大于变轨前的速度 | |
| D. | “神舟十号”变轨后的运行周期总小于变轨前的运行周期 |
13.下列关于曲线运动的说法正确的是( )
| A. | 速度不变的运动可能是曲线运动 | |
| B. | 速度变化的运动必定是曲线运动 | |
| C. | 加速度不变的运动可能是曲线运动 | |
| D. | 静止的物体在恒力作用下可能做曲线运动 |
20. 2011年11月3日凌晨1时43分,“神舟八号”与“天宫一号”在距地球表面343km的轨道上成功对接成组合体,如图所示.对于在轨道上运行的组合体,下列说法正确的是( )
2011年11月3日凌晨1时43分,“神舟八号”与“天宫一号”在距地球表面343km的轨道上成功对接成组合体,如图所示.对于在轨道上运行的组合体,下列说法正确的是( )
 2011年11月3日凌晨1时43分,“神舟八号”与“天宫一号”在距地球表面343km的轨道上成功对接成组合体,如图所示.对于在轨道上运行的组合体,下列说法正确的是( )
2011年11月3日凌晨1时43分,“神舟八号”与“天宫一号”在距地球表面343km的轨道上成功对接成组合体,如图所示.对于在轨道上运行的组合体,下列说法正确的是( )| A. | 不受地球引力作用 | B. | 运行周期为24 h | ||
| C. | 运行速度小于7.9 km/s | D. | 向心加速度大于9.8 m/s2 |
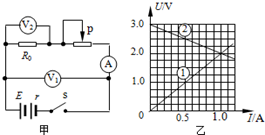
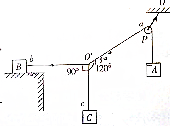 如图所示,物块A被绕过小滑轮P的细线所悬挂,小滑轮P被一根细线系于天花板上的O点,O点处安装一力传感器,质量为10kg的物块B放在粗糙的水平桌面上,bO′水平拉着物块B,CO′悬挂物块C,O′是三根线的结点,aO′、bO′与cO′夹角如图所示,细线、小滑轮的重力和细线与小滑轮间的摩擦力均可忽略,整个装置处于静止状态,若O点处安装的力传感器显示受到的拉力大小为F0=20$\sqrt{3}$N,物块B与水平桌面之间的动摩擦因数为0.2,重力加速度g=10m/s2,求:
如图所示,物块A被绕过小滑轮P的细线所悬挂,小滑轮P被一根细线系于天花板上的O点,O点处安装一力传感器,质量为10kg的物块B放在粗糙的水平桌面上,bO′水平拉着物块B,CO′悬挂物块C,O′是三根线的结点,aO′、bO′与cO′夹角如图所示,细线、小滑轮的重力和细线与小滑轮间的摩擦力均可忽略,整个装置处于静止状态,若O点处安装的力传感器显示受到的拉力大小为F0=20$\sqrt{3}$N,物块B与水平桌面之间的动摩擦因数为0.2,重力加速度g=10m/s2,求:

