题目内容
13.某同步卫星距地面高度为h,已知地球半径为R,表面的重力加速度为g,地球自转的角速度为ω,则该卫星的周期为( )| A. | 2π$\sqrt{\frac{R}{g}}$ | B. | $\frac{2π(R+h)}{R}$$\sqrt{\frac{R+h}{g}}$ | C. | $\frac{2πh}{R}$$\sqrt{\frac{R}{g}}$ | D. | $\frac{2π}{ω}$R |
分析 研究卫星绕地球做匀速圆周运动,根据万有引力提供向心力,列出等式,
在地球表面有万有引力等于重力列出等式,两等式联立表示出周期
解答 解:根据万有引力提供向心力列出等式,$\frac{GMm}{(R+h)^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$(R+h),
在地球表面有万有引力等于重力列出等式,$\frac{GMm}{{R}^{2}}$=mg
联立得:T=$\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$.
故选:B
点评 本题要求熟练应用万有引力提供向心力的各种表达形式,熟练掌握圆周运动的各个公式,题目难度较大

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
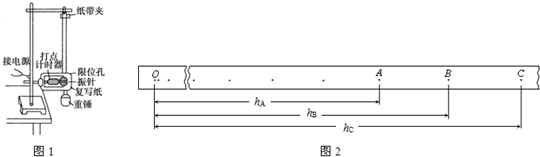
3.一列沿x正方向传播的简谐波t=0时刻的波形如图所示,t=0.2s时C点开始振动,则( )

| A. | t=0.3s,波向前传播了3m,质点B将到达质点C的位置 | |
| B. | t=0.05s,质点A的速度方向向上 | |
| C. | t=0到t=0.6s时间内,B质点的平均速度大小为10m/s | |
| D. | 产生这列波的波源的起振方向是向上的 |
1.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步.下列说法中正确的是( )
| A. | 开普勒通过对行星观测记录的研究发现了万有引力定律 | |
| B. | 卡文迪许测出了引力常量的数值 | |
| C. | 牛顿运动定律是自然界普遍适用的基本规律之一 | |
| D. | 牛顿应用“理想斜面实验”推翻了亚里士多德的“力是维持物体运动的原因”的观点 |
8.下列说法正确的是( )
| A. | 布朗运动只能在液体里发生,且温度越高,布朗运动越激烈 | |
| B. | 分子间距离增大,分子间作用力可能为斥力 | |
| C. | 分子动能与分子势能的和叫做这个分子的内能 | |
| D. | 滴进水中的墨水微粒能做扩散运动,说明分子间有空隙 | |
| E. | 外界对某理想气体做功2.0×105J,气体对外放热1.0×105J,则气体温度升高 |
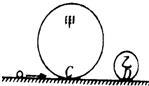 如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,运动一周后通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开乙轨道.若小球在两圆轨道的最高点对轨道的压力都恰好为零,求:
如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,运动一周后通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开乙轨道.若小球在两圆轨道的最高点对轨道的压力都恰好为零,求:
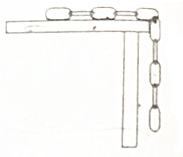 如图所示,一条质量为m,长为L的均匀铁链置于光滑水平桌面上,用手按住一端,使另一半下垂与桌边,放手后铁链下滑,当铁链全部脱离桌面的瞬间,重力对铁链做的功为$\frac{3mgL}{8}$;铁链的重力势能为-$\frac{mgL}{2}$(桌面高度h>L,取桌面为零势能参考平面).
如图所示,一条质量为m,长为L的均匀铁链置于光滑水平桌面上,用手按住一端,使另一半下垂与桌边,放手后铁链下滑,当铁链全部脱离桌面的瞬间,重力对铁链做的功为$\frac{3mgL}{8}$;铁链的重力势能为-$\frac{mgL}{2}$(桌面高度h>L,取桌面为零势能参考平面).