题目内容
4.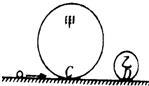 如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,运动一周后通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开乙轨道.若小球在两圆轨道的最高点对轨道的压力都恰好为零,求:
如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,运动一周后通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开乙轨道.若小球在两圆轨道的最高点对轨道的压力都恰好为零,求:(1)小球通过C点和D的速度大小.
(2)水平CD段的长度.
分析 (1)小球在两圆轨道的最高点对轨道的压力恰好为零,都由重力提供向心力,根据牛顿第二定律求出小球经过圆形轨道最高点时的速率.当小球从C到达甲圆形轨道的最高点的过程中,只有重力做功,根据机械能守恒定律求解小球经过C点时的速率,同理可求D点速度;
(2)根据动能定理求解CD的长度
解答 解:(1)设小球通过C点时的速度为vC,通过甲轨道最高点的速度为v1,
根据小球对轨道压力为零有
$mg=m\frac{{{v}_{1}}^{2}}{R}$…①
取轨道最低点所在水平面为参考平面,
由机械能守恒定律有$\frac{1}{2}m{{v}_{C}}^{2}=mg•2R+\frac{1}{2}m{{v}_{1}}^{2}$…②
联立①②式,可得${v}_{C}=\sqrt{5gR}$
同理可得小球通过D点时的速度${v}_{D}=\sqrt{5gr}$
(2)设CD段的长度为l,对小球通过CD
段的过程,由动能定理有
$-μmgl=\frac{1}{2}m{{v}_{D}}^{2}-\frac{1}{2}m{{v}_{C}}^{2}$
解得:
$l=\frac{5(R-r)}{2μ}$
答:(1)小球通过C点和D的速度大小分别为$\sqrt{5gR}$和$\sqrt{5gr}$.
(2)水平CD段的长度为$\frac{5(R-r)}{2μ}$.
点评 本题是向心力、机械能守恒定律、动能定理的综合应用.在竖直平面内,小球沿光滑圆轨道的运动模型与轻绳拴的球的运动模型相似,难度适中.

练习册系列答案
相关题目
2.下列说法中正确的是( )
| A. | 物体在恒力作用下不可能作曲线运动 | |
| B. | 物体在恒力作用下有可能作曲线运动 | |
| C. | 物体在变力作用下不可能作直线运动 | |
| D. | 物体在变力作用下有可能作直线运动 |
15. 如图所示,A、B、C、D是一匀强电场的四个等差等势面,B为零势面,一个带电粒子(不计重力),只在电场力作用下从等势面A上一点以0.24J的初动能垂直于等势面向右运动.粒子到达等势面D时速度恰好为零.则当粒子的电势能为0.1J时所具有的动能为( )
如图所示,A、B、C、D是一匀强电场的四个等差等势面,B为零势面,一个带电粒子(不计重力),只在电场力作用下从等势面A上一点以0.24J的初动能垂直于等势面向右运动.粒子到达等势面D时速度恰好为零.则当粒子的电势能为0.1J时所具有的动能为( )
 如图所示,A、B、C、D是一匀强电场的四个等差等势面,B为零势面,一个带电粒子(不计重力),只在电场力作用下从等势面A上一点以0.24J的初动能垂直于等势面向右运动.粒子到达等势面D时速度恰好为零.则当粒子的电势能为0.1J时所具有的动能为( )
如图所示,A、B、C、D是一匀强电场的四个等差等势面,B为零势面,一个带电粒子(不计重力),只在电场力作用下从等势面A上一点以0.24J的初动能垂直于等势面向右运动.粒子到达等势面D时速度恰好为零.则当粒子的电势能为0.1J时所具有的动能为( )| A. | 0.14J | B. | 0.16J | C. | 0.06J | D. | 0.22J |
12.线圈在匀强磁场中匀速转动,产生的交变电流如图,则( )
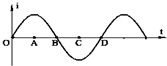

| A. | 在A和C时刻线圈平面和磁场垂直 | |
| B. | 在A和C时刻线圈磁通量变化率为零 | |
| C. | 在B时刻线圈中的磁通量为零 | |
| D. | 若线圈转动的周期为0.02s,则该交变电流的频率为50Hz |
19.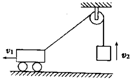 如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )
如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )
 如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )
如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )| A. | 物体做匀速直线运动,且v1=v2 | B. | 物体做加速直线运动,且v2>v1 | ||
| C. | 物体做加速直线运动,且FT>G | D. | 物体做匀速直线运动,且FT=G |
9. 如图,平行板电容器两个极板与水平地面成2α角,在平行板间存在着匀强电场,直线CD是两板间一条垂直于板的直线,竖直线EF与CD交于O点,一个带电小球沿着∠FOD的角平分线从A点经O点向B点做直线运动,重力加速度为g.则在此过程中,下列说法正确的是( )
如图,平行板电容器两个极板与水平地面成2α角,在平行板间存在着匀强电场,直线CD是两板间一条垂直于板的直线,竖直线EF与CD交于O点,一个带电小球沿着∠FOD的角平分线从A点经O点向B点做直线运动,重力加速度为g.则在此过程中,下列说法正确的是( )
 如图,平行板电容器两个极板与水平地面成2α角,在平行板间存在着匀强电场,直线CD是两板间一条垂直于板的直线,竖直线EF与CD交于O点,一个带电小球沿着∠FOD的角平分线从A点经O点向B点做直线运动,重力加速度为g.则在此过程中,下列说法正确的是( )
如图,平行板电容器两个极板与水平地面成2α角,在平行板间存在着匀强电场,直线CD是两板间一条垂直于板的直线,竖直线EF与CD交于O点,一个带电小球沿着∠FOD的角平分线从A点经O点向B点做直线运动,重力加速度为g.则在此过程中,下列说法正确的是( )| A. | 小球可能带正电,也可能带负电 | |
| B. | 小球可能做匀加速直线运动 | |
| C. | 小球加速度大小为gcosα | |
| D. | 小球重力势能的增加量等于电势能的增加量 |
16.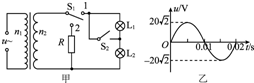 图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常发光的功率为P.下列说法正确的是( )
图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常发光的功率为P.下列说法正确的是( )
 图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常发光的功率为P.下列说法正确的是( )
图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常发光的功率为P.下列说法正确的是( )| A. | 输入电压u的表达式u=20$\sqrt{2}$sin50πt(V) | |
| B. | 只断开S2后,L1、L2的功率均小于$\frac{P}{4}$ | |
| C. | 只断开S2后,原线圈的输入功率大于$\frac{P}{2}$ | |
| D. | 若S1换接到2后,R消耗的电功率为0.8W |
13.某同步卫星距地面高度为h,已知地球半径为R,表面的重力加速度为g,地球自转的角速度为ω,则该卫星的周期为( )
| A. | 2π$\sqrt{\frac{R}{g}}$ | B. | $\frac{2π(R+h)}{R}$$\sqrt{\frac{R+h}{g}}$ | C. | $\frac{2πh}{R}$$\sqrt{\frac{R}{g}}$ | D. | $\frac{2π}{ω}$R |