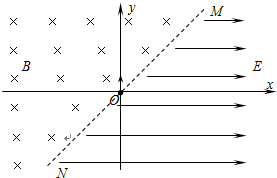题目内容
如图所示，xoy为竖直平面内的一个直角坐标系，y为竖直方向，OA为竖直平面内的光滑抛物线轨道，其方程为：
（式中x、y的单位均是国际单位m），将一个质量为m的光滑小环穿在此轨道上，从O点由静止状态沿着此轨道下滑，P是抛物线轨道上的一点，已知O和P两点连线与竖直方向的夹角为45°，求小环通过P点时的速度大小和方向.（重力加速度g=10m/s2）
过P点的速度方向与y轴的夹角为：
解析:
设P的坐标为（xP，yp），
则依题意得：
， 
解得：
小环沿轨道下滑时机械能守恒，设到达P点时速度大小为vp，根据机械能守恒定律得： 
解得：
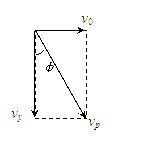vp的方向沿着轨迹的切线方向，即与沿着
的轨迹做平抛运动的物体经过P点时的速度方向相同.
设某物体从O点以v0做平抛运动，由
，
，
解得：
，vy=10m/s
所以，过P点的速度方向与y轴的夹角为：
练习册系列答案
相关题目
（2011?江苏模拟）如图所示，xoy为竖直平面直角坐标系，MN为第Ⅰ、第Ⅲ象限的平分线，在MN的左侧有垂直于坐标平面水平向里的匀强磁场，磁感应强度B=0.1T，在MN右侧有水平向右的匀强电场，电场强度大小E=2N/C．现有一个带负电的微粒，从坐标原点O沿y轴正方向以v0=80m/s的初速度射入磁场，已知微粒的带电量为q=2×10-12C，质量为m=5×10-16kg，试求：
