题目内容
（2011?江苏模拟）如图所示，xoy为竖直平面直角坐标系，MN为第Ⅰ、第Ⅲ象限的平分线，在MN的左侧有垂直于坐标平面水平向里的匀强磁场，磁感应强度B=0.1T，在MN右侧有水平向右的匀强电场，电场强度大小E=2N/C．现有一个带负电的微粒，从坐标原点O沿y轴正方向以v0=80m/s的初速度射入磁场，已知微粒的带电量为q=2×10-12C，质量为m=5×10-16kg，试求：（1）带电微粒第一次离开磁场区时的位置坐标；
（2）带电微粒第一次越过y轴时的位置坐标；
（3）带电微粒从O点射出到第一次越过y轴时所经历的时间是多长．
分析：（1）带电微粒从O点射入磁场，运动轨迹如图，第一次经过磁场边界上的A点，由洛伦兹力公式和牛顿第二定律即可求解；
（2）微粒从C点沿y轴正方向进入电场，做类平抛运动，根据平抛运动得基本公式即可求解．
（3）根据圆周运动的周期公式及粒子在磁场中的运动轨迹即可解题；
（2）微粒从C点沿y轴正方向进入电场，做类平抛运动，根据平抛运动得基本公式即可求解．
（3）根据圆周运动的周期公式及粒子在磁场中的运动轨迹即可解题；
解答：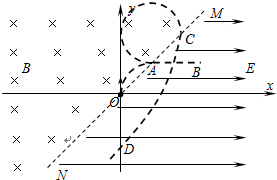
解析：
（1）从题设数据中，可以发现微粒重子与电场力和洛伦兹力相比太小，应忽略不计．带电微粒从O点射入磁场后，运动轨迹如图所示．
微粒在磁场中运动过程中：
由qv0B=m
得 r=
=0.2m
故第一次离开磁场区时的位置A点位置坐标为（0.2m，0.2m）
（2）当微粒从C点离开磁场区时，速度方向竖直向下，在电场力作用下做类平抛运动到达D点，则：
解得微粒从C到D过程中运动时间为：tCD=1×10-2（s）
D点的纵坐标y=0.4（m）
故带电微粒第一次越过y轴时的位置坐标为（0，0.4m）
（3）微粒在磁场中做圆周运动的周期为T=
则微粒在磁场运动的总时间：tOA+tAC=
T+
T=1.57×10-2（s）
微粒在电场中运动时间：tAB=2
=
=2×10-2（s）
故微粒从O点射出到第一次越过y轴时所经历的时间t=tOA+tAB+tAC+tCD=4.57×10-2（s）
答：（1）带电微粒第一次离开磁场区时的位置坐标为（0.2m，0.2m）
（2）带电微粒第一次越过y轴时的位置坐标为（0，0.4m）
（3）带电微粒从O点射出到第一次越过y轴时所经历的时间是4.57×10-2（s）
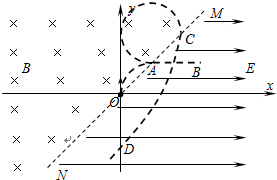解析：（1）从题设数据中，可以发现微粒重子与电场力和洛伦兹力相比太小，应忽略不计．带电微粒从O点射入磁场后，运动轨迹如图所示．
微粒在磁场中运动过程中：
由qv0B=m
| v02 |
| r |
| mv0 |
| qB |
故第一次离开磁场区时的位置A点位置坐标为（0.2m，0.2m）
（2）当微粒从C点离开磁场区时，速度方向竖直向下，在电场力作用下做类平抛运动到达D点，则：
|
解得微粒从C到D过程中运动时间为：tCD=1×10-2（s）
D点的纵坐标y=0.4（m）
故带电微粒第一次越过y轴时的位置坐标为（0，0.4m）
（3）微粒在磁场中做圆周运动的周期为T=
| 2πm |
| qB |
则微粒在磁场运动的总时间：tOA+tAC=
| 1 |
| 4 |
| 3 |
| 4 |
微粒在电场中运动时间：tAB=2
| v0 |
| a |
| 2mv0 |
| qE |
故微粒从O点射出到第一次越过y轴时所经历的时间t=tOA+tAB+tAC+tCD=4.57×10-2（s）
答：（1）带电微粒第一次离开磁场区时的位置坐标为（0.2m，0.2m）
（2）带电微粒第一次越过y轴时的位置坐标为（0，0.4m）
（3）带电微粒从O点射出到第一次越过y轴时所经历的时间是4.57×10-2（s）
点评：本题主要考查了带电粒子在混合场中运动的问题，要求同学们能正确分析粒子的受力情况，再通过受力情况分析粒子的运动情况，熟练掌握圆周运动及平抛运动的基本公式，难度适中．
练习册系列答案
相关题目
（2011?江苏模拟）如图所示电路，将两个相同的电流计分别改装成电流表A1（0～3A）和电流表A2（0～0.6A），把这两个电流表并连接入电路中测量电流．则下列说法中正确的是（ ）
（2011?江苏模拟）利用霍尔效应制作的霍尔元件，广泛应用于测量和自动控制等领域．如图是霍尔元件的工作原理示意图，磁感应强度B垂直于霍尔元件的工作面向下，通入图示方向的电流I，C、D两侧面会形成电势差UCD，下列说法中正确的是（ ）