题目内容
如图所示,坐标系xOy位于竖直平面内,所在空间有沿水平方向垂直于纸面向里的匀强磁场,磁感应强度大小为B,在x<0的空间内还有沿x轴负方向的匀强电场,场强大小为E.一个带电油滴经图中x轴上的M点,沿着直线MP做匀速运动,图中α=30°,经过P点后油滴进入x>0的区域,要使油滴在x>0的区域内做匀速圆周运动,需在该区域内加一个匀强电场.若带电油滴沿PN做匀速圆周运动,并垂直于x轴通过轴上的N点.已知重力加速度为g.
(1)判断油滴的带电性质;
(2)求油滴运动的速率;
(3)求在x>0的区域内所加电场的场强;
(4)求油滴从M点出发运动到N点所用的时间.
解析:(1)油滴带正电.
(2)油滴受三力作用(见图)沿直线匀速运动
由平衡条件有qvBsin30°=qE ①
mgtan30°=qE ②
由①式解得v=
. ③
(3)在x>0的区域,油滴要做匀速圆周运动,其所受的电场力必与重力平衡,由于油滴带正电,所以场强方向竖直向上.
设该电场的场强为E′,则有qE′=mg ④
②④式联立解得E′=
E. ⑤
(4)见下图,?
为油滴做圆周运动在x>0、y<0 区域内形成的圆弧轨道所对应的弦,PO′是过P点所作的垂直于MP的直线,由于MO=NO,由几何关系容易知道O′点一定是圆心,且∠PO′N=120° ⑥
设油滴从M点到P点和从P点到N点经历的时间分别为t1和t2
做匀速圆周运动时有qvB=
⑦
由②③⑦式解得R=
⑧
t1=
⑨
t2=
⑩
全过程经历的时间为t=t1+t2=
. 11
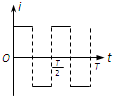
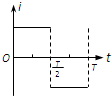
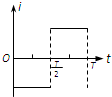
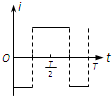
（2013?温州一模）两个相距很近的等量异种点电荷组成的系统称为电偶极子．设相距为l，电荷量分别为+q和-q的点电荷构成电偶极子，如图所示．取二者连线方向为y轴方向，中点O为原点，建立如图所示的xOy坐标系，p点距坐标原点O的距离为r（r＞＞l），p、O两点间的连线与y轴正方向的夹角为θ，设无穷远处的电势为零，p点的电势为φ，真空中静电力常量为k．下面给出φ的四个表达式，其中只有一个是合理的．你可能不会求解p点的电势φ，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断．根据你的判断，φ的合理表达式应为（ ）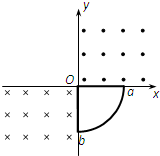
如图所示，xOy坐标系第一象限内有垂直纸面向外的匀强磁场，第三象限内有垂直纸面向里的匀强磁场，磁感强度大小均为B，第二、四象限内没有磁场．一个围成四分之一圆弧形的导体环Oab，其圆心在原点O，开始时导体环在第四象限，且导体环两边oa、ob恰好分别与x轴、y轴重合，从t=0时刻开始导体环绕O点在xOy坐标平面内逆时针匀速转动．规定逆时针方向为电流的正方向，在导体环转动一周的过程中，下列能正确表示环内感应电流i随时间t变化的图象是（ ）
