题目内容
3. 质量均为m的两物块A和B之间连接着一个轻质弹簧,其劲度系数为k,现将物块A、B放在水平地面上一斜面的等高处,如图所示,弹簧处于压缩状态,且物体与斜面均能保持静止,已知斜面的倾角为θ,两物块和斜面间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )
质量均为m的两物块A和B之间连接着一个轻质弹簧,其劲度系数为k,现将物块A、B放在水平地面上一斜面的等高处,如图所示,弹簧处于压缩状态,且物体与斜面均能保持静止,已知斜面的倾角为θ,两物块和斜面间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )| A. | 斜面和水平地面间一定有静摩擦力 | |
| B. | 斜面对 A、B组成的系统的静摩擦力的合力为2mgsinθ | |
| C. | 若将弹簧拿掉,物块有可能发生滑动 | |
| D. | 弹簧的最大压缩量为$\frac{{mg\sqrt{μ^2{cos}^2θ-{sin}^2θ}}}{k}$ |
分析 对整体进行分析,根据平衡条件可分析物体是否会发生滑动,从而明确摩擦力大小;
对物体进行分析,当物体平衡时,受重力、支持力和弹簧的弹力,三力平衡,根据平衡条件并结合正交分解法和胡克定律列式求解;
解答 解:A、对整体分析可知,整体在水平方向不受外力,故地面不受静摩擦力;故A错误;
B、对AB及弹簧组成的系统分析可知,整体受重力、支持力和斜面的摩擦力,则摩擦力大小为2mgsinθ;故B正确;
C、开始时单个物体受到的静摩擦力大于重力沿斜面向下的分力;由于物体受到的为静摩擦力,若将弹簧拿掉,摩擦力瞬间发生变化;与重力的分力大小相等;不可能使物块发生滑动;故C错误;
D、物块静止在斜面上,在斜面这个平面内共有三个力作用在物体上,一个是重力沿斜面向下的分力mgsinθ,静摩擦力f≤fm=μmgcosθ,方向不确定,弹簧弹力水平方向kx,则弹力等于mgsinθ和静摩擦力f的合力,当静摩擦力最大时,合力最大,此时:kx=$\sqrt{{f}_{m}^{2}-{(mgsinθ)}^{2}}$
故x=$\frac{mg\sqrt{(μcosθ)^{2}-si{n}^{2}θ}}{k}$; 故D正确;
故选:BD.
点评 本题关键是先对物块受力分析,根据平衡条件并结合正交分解法和胡克定律列式求解求解弹簧最大伸长量,灵活性较强;注意正确选择研究对象进行分析.

练习册系列答案
相关题目
14. 如图所示,水平放置的带电电容器ab之间有垂直纸面的匀强磁场,有一束质量、速度和电荷量不全相等的离子(重力不计)垂直磁场方向进入正交的匀强电场和匀强磁场区域,做直线运动后,进入另一个匀强磁场中并分裂为A、B两束,下列说法中正确的是( )
如图所示,水平放置的带电电容器ab之间有垂直纸面的匀强磁场,有一束质量、速度和电荷量不全相等的离子(重力不计)垂直磁场方向进入正交的匀强电场和匀强磁场区域,做直线运动后,进入另一个匀强磁场中并分裂为A、B两束,下列说法中正确的是( )
 如图所示,水平放置的带电电容器ab之间有垂直纸面的匀强磁场,有一束质量、速度和电荷量不全相等的离子(重力不计)垂直磁场方向进入正交的匀强电场和匀强磁场区域,做直线运动后,进入另一个匀强磁场中并分裂为A、B两束,下列说法中正确的是( )
如图所示,水平放置的带电电容器ab之间有垂直纸面的匀强磁场,有一束质量、速度和电荷量不全相等的离子(重力不计)垂直磁场方向进入正交的匀强电场和匀强磁场区域,做直线运动后,进入另一个匀强磁场中并分裂为A、B两束,下列说法中正确的是( )| A. | 组成A、B束的离子都带正电 | |
| B. | 组成A、B束的离子质量一定不同 | |
| C. | 电容器之间的磁场方向垂直纸面向里 | |
| D. | A束离子的比荷($\frac{q}{m}$)大于B束离子的比荷 |
11.解决物理疑难问题的过程,往往伴随新理论的建立,在物理学史中,下列现象与物理新理论的建立不存在必然联系的是( )
| A. | 行星绕太阳运动与万有引力 | B. | 电荷间作用力与电场 | ||
| C. | 光电效应现象与光子说 | D. | 氢原子光谱与质能方程 |
18.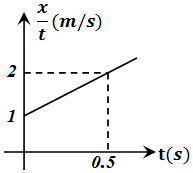 一质点沿一直线运动,以运动起点作为位移参考点并开始计时,设在时间t内所发生的位移为x,其$\frac{x}{t}$-t图象如图所示,则由图可知( )
一质点沿一直线运动,以运动起点作为位移参考点并开始计时,设在时间t内所发生的位移为x,其$\frac{x}{t}$-t图象如图所示,则由图可知( )
 一质点沿一直线运动,以运动起点作为位移参考点并开始计时,设在时间t内所发生的位移为x,其$\frac{x}{t}$-t图象如图所示,则由图可知( )
一质点沿一直线运动,以运动起点作为位移参考点并开始计时,设在时间t内所发生的位移为x,其$\frac{x}{t}$-t图象如图所示,则由图可知( )| A. | 质点的初速度为1m/s | B. | 质点的初速度为0.5m/s | ||
| C. | 质点的加速度为2m/s2 | D. | 质点的加速度为4m/S2 |
15. 如图所示,地面上固定一个斜面,上面叠放着A、B两个物块并均处于静止状态.现对物块A施加一个斜向上的力F作用,A、B两个物块始终处于静止状态.则木块B的受力个数可能是( )
如图所示,地面上固定一个斜面,上面叠放着A、B两个物块并均处于静止状态.现对物块A施加一个斜向上的力F作用,A、B两个物块始终处于静止状态.则木块B的受力个数可能是( )
 如图所示,地面上固定一个斜面,上面叠放着A、B两个物块并均处于静止状态.现对物块A施加一个斜向上的力F作用,A、B两个物块始终处于静止状态.则木块B的受力个数可能是( )
如图所示,地面上固定一个斜面,上面叠放着A、B两个物块并均处于静止状态.现对物块A施加一个斜向上的力F作用,A、B两个物块始终处于静止状态.则木块B的受力个数可能是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
12.探测火星一直是人类的梦想,若在未来某个时刻,人类乘飞船来到了火星,宇航员先乘飞船绕火星做圆周运动,测出飞船坐圆周运动时离火星表面的高度为H,环绕的周期为T及环绕的线速度为v,引力常量为G,由此可得出( )
| A. | 火星的半径为$\frac{vT}{2π}$ | |
| B. | 火星表面的重力加速度为$\frac{{2πT{v^3}}}{{{{(vT-2πH)}^2}}}$ | |
| C. | 火星的质量为$\frac{{T{v^2}}}{2πG}$ | |
| D. | 火星的第一宇宙速度为$\sqrt{\frac{{4{π^2}{v^2}T}}{{G{{(vT-πH)}^3}}}}$ |
19. 如图所示,质量为m的小球用水平弹簧系住,并用细绳AB和一端带滑轮的光滑木板OB托住,质量为M的木板与竖直墙壁的夹角为60°,小球恰好处于静止状态.当剪断细绳AB,木板绕O顺时针转动瞬间,小球的加速度大小为( )
如图所示,质量为m的小球用水平弹簧系住,并用细绳AB和一端带滑轮的光滑木板OB托住,质量为M的木板与竖直墙壁的夹角为60°,小球恰好处于静止状态.当剪断细绳AB,木板绕O顺时针转动瞬间,小球的加速度大小为( )
 如图所示,质量为m的小球用水平弹簧系住,并用细绳AB和一端带滑轮的光滑木板OB托住,质量为M的木板与竖直墙壁的夹角为60°,小球恰好处于静止状态.当剪断细绳AB,木板绕O顺时针转动瞬间,小球的加速度大小为( )
如图所示,质量为m的小球用水平弹簧系住,并用细绳AB和一端带滑轮的光滑木板OB托住,质量为M的木板与竖直墙壁的夹角为60°,小球恰好处于静止状态.当剪断细绳AB,木板绕O顺时针转动瞬间,小球的加速度大小为( )| A. | 0 | B. | g | C. | $\frac{\sqrt{3}}{3}$g | D. | $\frac{2\sqrt{3}}{3}$g |
 如图所示,升降机中固定一光滑斜面,倾角α=30°,斜面上弹簧的下端连接着质量m=4kg的木块,当升降机以2m/s2的加速度加速下降时(g取10m/s2).求:
如图所示,升降机中固定一光滑斜面,倾角α=30°,斜面上弹簧的下端连接着质量m=4kg的木块,当升降机以2m/s2的加速度加速下降时(g取10m/s2).求: