题目内容
如图(a)所示,A、B为钉在光滑水平面上的两根细铁钉,可视为质点的小球C用细绳拴在铁钉B上(细绳能承受足够大的拉力),A、B、C在同一直线上。t=0时,给小球一个垂直于绳的速度,使小球绕着两根铁钉在水平面上做圆周运动,每次细绳碰到钉子均无机械能损失。在0≤t≤10s时间内,细绳的拉力随时间变化的规律如图(b)所示,则下列说法中正确的有( )
A.t=10s时刻细绳第二次碰到钉子
B.t=11s时刻细绳第二次碰到钉子
C.t=11.5s时刻细绳拉力大小为7.5N
D.细绳第三次碰钉子到第四次碰钉子的时间间隔为3s
BCD
解析试题分析:由图可知,在0~6s内绳子的拉力不变,有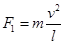 ,6~10s内的拉力不变,有
,6~10s内的拉力不变,有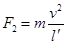 ,联立解得
,联立解得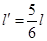 ,即两钉子间的距离为
,即两钉子间的距离为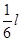 ,第一个半圈经历的时间为6s,则
,第一个半圈经历的时间为6s,则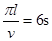 ,则第二个半圈所用的时间
,则第二个半圈所用的时间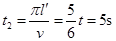 ,故A错误、B正确;第三个半圈所用的时间
,故A错误、B正确;第三个半圈所用的时间 ,则
,则 时,小球的转动半径
时,小球的转动半径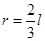 ,根据
,根据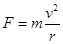 可知拉力变为开始时的
可知拉力变为开始时的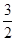 倍,大小为7.5N,所以C正确;由上可知,细绳每跟钉子碰撞一次,转动半圈的时间减小
倍,大小为7.5N,所以C正确;由上可知,细绳每跟钉子碰撞一次,转动半圈的时间减小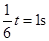 ,则细绳第三次碰钉子到第四次碰钉子的时间间隔为
,则细绳第三次碰钉子到第四次碰钉子的时间间隔为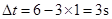 ,所以选项D正确;
,所以选项D正确;
考点:圆周运动、牛顿第二定律

如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,而后释放,摆球运动过程中,支架始终不动,以下说法正确的是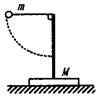
| A.在释放瞬间,支架对地面压力为(m+M)g |
| B.在释放瞬间,支架对地面压力为Mg |
| C.摆球到达最低点时,支架对地面压力为(m+M)g |
| D.摆球到达最低点时,支架对地面压力为(3m+M)g |
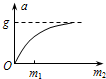
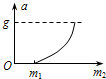
一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图甲所示,现在最低点处给小球一初速度,使其绕O点在竖直平面内做圆周运动,通过传感器记录下绳中拉力大小F随时间t的变化规律如图乙所示,已知F1的大小等于7F2,引力常量为G,各种阻力不计,则( )
A.该星球表面的重力加速度为 |
B.卫星绕该星球的第一宇宙速度为 |
C.该星球的质量为 |
| D.小球通过最高点的最小速度为零 |
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为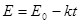 (
(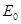 、
、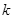 均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为
均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为 ,已知
,已知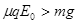 。
。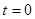 时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑 后脱离墙面,此时速度大小为
后脱离墙面,此时速度大小为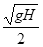 ,最终落在地面上。则下列关于物体的运动说法正确的是( )
,最终落在地面上。则下列关于物体的运动说法正确的是( )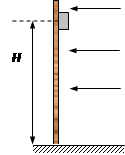
| A.当物体沿墙壁下滑时,物体先加速再做匀速直线运动 |
| B.物体从脱离墙壁到落地之前的运动轨迹是一段直线 |
C.物体克服摩擦力所做的功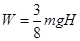 |
D.物体与墙壁脱离的时刻为 |
如图所示,一小球m自空中自由下落,落到正下方的直立轻弹簧上与其A端接触并连接在一起。从小球与弹簧A端接触到继续压缩弹簧直到小球降至最低位置的过程中,下列关于小球运动状态描述正确的是
| A.小球作减速运动,加速度越来越大,速度越来越小最后等于零 |
| B.小球加速度先减小后增大,速度先增大后减小为零 |
| C.小球的速度和加速度为零时弹簧的压缩量最大 |
| D.小球加速度的最大值为g |
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和小球B紧贴圆锥筒内壁分别在水平面内做匀速圆周运动,则下列说法中正确的是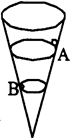
| A.A球的线速度必定小于B球的线速度 |
| B.A球的角速度必定大于B球的角速度 |
| C.A球运动的周期必定大于B球的周期 |
| D.A球对筒壁的压力必定大于B球对筒壁的压力 |
如图所示,弹簧左端固定,右端自由伸长到O点并系住物体m.现将弹簧压缩到A点,然后释放,物体一直可以运动到B点,如果物体受到地面的阻力恒定,则 ( )
| A.物体从A到O先加速后减速 |
| B.物体从A到O加速运动,从O到B减速运动 |
| C.物体运动到O点时所受合力为0 |
| D.物体从A到O的过程加速度逐渐减小 |