题目内容
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和小球B紧贴圆锥筒内壁分别在水平面内做匀速圆周运动,则下列说法中正确的是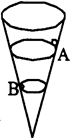
| A.A球的线速度必定小于B球的线速度 |
| B.A球的角速度必定大于B球的角速度 |
| C.A球运动的周期必定大于B球的周期 |
| D.A球对筒壁的压力必定大于B球对筒壁的压力 |
C
解析试题分析:两球所受重力大小相等,支持力方向相同,根据力的合成,知两支持力大小相等,合力大小相等,根据牛顿第三定律,AB球对筒壁的压力大小相等,D错误;根据 ,合力相等、质量相等,r越大,线速度越大,所以A球的线速度大于B球的线速度,A错误;根据
,合力相等、质量相等,r越大,线速度越大,所以A球的线速度大于B球的线速度,A错误;根据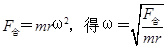 ,r越大,角速度越小,B错误;根据
,r越大,角速度越小,B错误;根据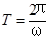 得ω越大,周期越小,C正确。
得ω越大,周期越小,C正确。
考点:本题考查牛顿第二定律在圆周运动中的应用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
低碳、环保是未来汽车的发展方向.某汽车研发机构在汽车的车轮上安装了小型发电机,将减速时的部分动能转化并储存在蓄电池中,以达到节能的目的.某次测试中,汽车以额定功率行驶一段距离后关闭发动机,测出了汽车动能Ek与位移x的关系图象如图,其中①是关闭储能装置时的关系图线,②是开启储能装置时的关系图线.已知汽车的质量为1 000 kg,设汽车运动过程中所受地面阻力恒定,空气阻力不计.根据图象所给的信息可求出( )
| A.汽车行驶过程中所受地面的阻力为1 000 N |
| B.汽车的额定功率为80 kW |
| C.汽车加速运动的时间为22.5 s |
| D.汽车开启储能装置后向蓄电池提供的电能为5×107 J |
如图,质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q,当剪断Ⅱ的瞬间,小球的加速度a应是
| A.大小a=g |
B.大小a="g" tan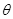 |
| C.方向水平向左 |
| D.方向竖直向下 |
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,由此可以确定
| A.滑块下滑和上滑过程加速度的大小a1、a2 |
| B.滑块最终所处的位置 |
| C.滑块与杆之间动摩擦因数μ |
| D.滑块第k次与挡板碰撞后速度vk |

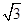 , 两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间:
, 两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间:
 , B球加速度为
, B球加速度为
 , B球加速度为
, B球加速度为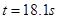 , B球加速度为
, B球加速度为










