题目内容
(14分)如图所示,两平行金属板A、B长8cm,两板间距离d=8cm,A板比B板电势高300V,一带正电的粒子电荷量q=10-10C,质量m=10-20kg,沿电场中心线RO垂直电场线飞入电场,初速度υ0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响),已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上.(静电力常数k = 9.0×109N·m2/C2)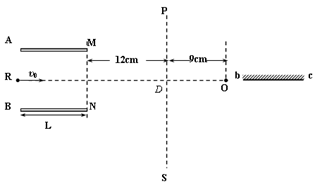
(1)求粒子穿过界面MN时偏离中心线RO的距离多远?到达PS界面时离D点多远?
(2)在图上粗略画出粒子运动的轨迹.
(3)确定点电荷Q的电性并求其电荷量的大小.(结果保留2位有效数字)
(1)0.03m;0.12m;(2)运动的轨迹见下图;(3)负电性;1.04×10-8C。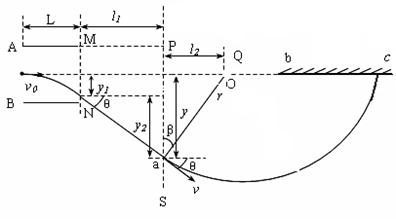
解析试题解析:(1)带电粒子穿过界面MN时偏离中心线的距离,即侧向位移: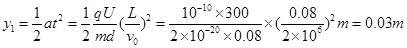 (3分)
(3分)
带电粒子的速度离开电场时的速度及穿过PS进入点电荷电场的速度:
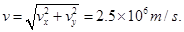
此时的速度方向与水平方向成θ,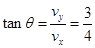
带电粒子在离开电场后将做匀速直线运动打在PS上的a点(如图),则a点离中心线的距离为y:则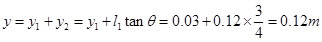 (2分)
(2分)
(2)轨迹如图所示。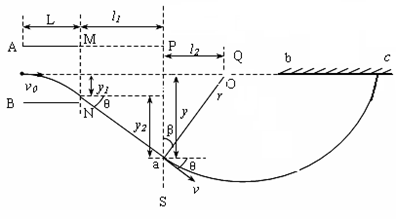
(3)a点与点电荷所在位置的连线与PS的夹角为β,则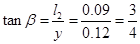 ,
,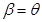 ,
,
带电粒子进入点电荷的电场时,速度与点电荷对粒子的库仑力垂直,由题的描述:粒子穿过界面PS最后垂直打在荧光屏bc上,由此可以做出判断:该带电粒子在穿过界面PS后将绕点电荷Q作匀速圆周运动。
带正电的粒子必定受到Q的吸引力,所以Q带负电。
半径r=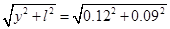 m=0.15m;
m=0.15m;
由库仑定律和匀速圆周运动规律可得:k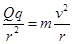 得:
得:
Q=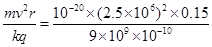 C=1.04×10-8C
C=1.04×10-8C
考点:带电粒子在电场中的运动,牛顿第二定律,库仑定律等。

 ,sin37o=0.6,cos37o=0.8,g=10m/s2。求:
,sin37o=0.6,cos37o=0.8,g=10m/s2。求: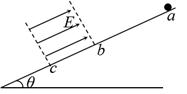
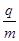 =2.0×106C/kg,粒子重力不计,计算结果保留两位有效数字。求:
=2.0×106C/kg,粒子重力不计,计算结果保留两位有效数字。求: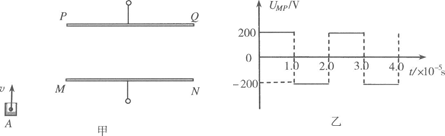
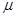 ,最大静摩擦力等于滑动摩擦力大小,A、B、C(连同挡板P)的质量都为
,最大静摩擦力等于滑动摩擦力大小,A、B、C(连同挡板P)的质量都为 ,开始时,B和C静止,A以某一初速度
,开始时,B和C静止,A以某一初速度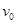 向右运动,重力加速度为
向右运动,重力加速度为 .求:
.求: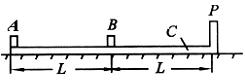

 .
.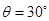 的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数
的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数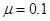 ,取g=10m/s2.
,取g=10m/s2.
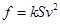 (其中k为比例系数).雨点接近地面时近似看做匀速直线运动,重力加速度为g.若把雨点看做球形,其半径为r,球的体积为
(其中k为比例系数).雨点接近地面时近似看做匀速直线运动,重力加速度为g.若把雨点看做球形,其半径为r,球的体积为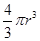 ,设雨点的密度为
,设雨点的密度为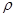 ,求:
,求: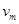 (用
(用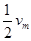 时,雨点的加速度a为多大?
时,雨点的加速度a为多大?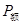 =10.0W,赛车的质量m=1.0kg,在水平直轨道上受到的阻力f=2.0N,AB段长L=10.0m,BE的高度差h=1.25m,BE的水平距离x=1.5m。若赛车车长不计,忽略空气阻力,g取10m/s2.
=10.0W,赛车的质量m=1.0kg,在水平直轨道上受到的阻力f=2.0N,AB段长L=10.0m,BE的高度差h=1.25m,BE的水平距离x=1.5m。若赛车车长不计,忽略空气阻力,g取10m/s2.