题目内容
如图所示,小球(可视为质点)带电量为q=1×10-2C,质量为m=2×10-2kg,放在一个倾角为θ=37o的足够长绝缘斜面上。斜面bc部分光滑,其它部分粗糙,且小球与斜面间的动摩擦因数μ=0.5,bc段有一平行斜面向上的有界匀强电场。现让小球从a点由静止释放,经过t=0.3s,到达c点。已知ab的长度为L=4cm,bc的长度为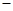 ,sin37o=0.6,cos37o=0.8,g=10m/s2。求:
,sin37o=0.6,cos37o=0.8,g=10m/s2。求: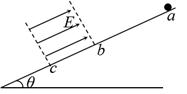
(1)匀强电场场强E的大小;
(2)小球第一次沿斜面向上运动的最高点到b点的距离。
(1) 20N/C (2) 0.8m
解析试题分析: (1) 设匀强电场场强大小为E,则由a到b,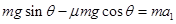
 ,b点的速度
,b点的速度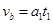
由b到c,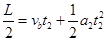
由题意,t1+t2=t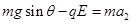
解得:E=20N/C
(2) 小球到达c点的速度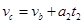 ,解得,
,解得,
设小球第一次沿斜面向上运动的最高点到b点的距离为x,
c到最高点,由动能定理得, 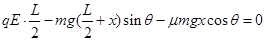
或者,b到最高点,由动能定理得,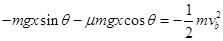
解得,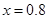 cm
cm
考点:动能定理及牛顿定律的应用。

练习册系列答案
相关题目
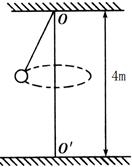


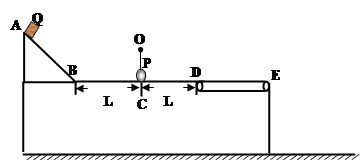
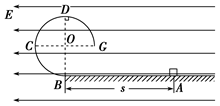
 圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为
圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为