题目内容
【题目】如图所示，小球A置于固定在水平面上的光滑半圆柱体上，小球B用水平轻弹簧拉着系于竖直板上，两小球A、B通过光滑滑轮O用轻质细线相连，两球均处于静止状态，已知B球质量为m，O点在半圆柱体圆心O1的正上方，OA与竖直方向成30°角，OA长度与半圆柱体半径相等，OB与竖直方向成45°角，则下列叙述正确的是
A. 小球A、B受到的拉力TOA与TOB相等，且TOA＝TOB＝
B. 弹簧弹力大小
C. A球质量为
D. 光滑半圆柱体对A球支持力的大小为mg
【答案】C
【解析】
A、B、隔离对B分析，根据共点力平衡得：
水平方向有：TOBsin45°=F
竖直方向有：TOBcos45°=mg，
则
，弹簧弹力 F=mg，
根据定滑轮的特性知：TOA与TOB相等；故A，B错误.
C、D、对A分析，如图所示：
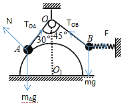
由几何关系可知拉力TOA和支持力N与水平方向的夹角相等，夹角为60°，则N和T相等，有：2TOAsin60°=mAg，
解得：
，由对称性可得：
，故C正确，D错误.
故选C.
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
