题目内容
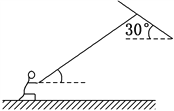
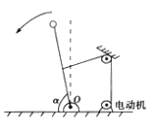
【题目】如图所示，长为2L的轻杆上端固定一质量为m的小球，下端用光滑铰链连接于地面上的O点，杆可绕O点在竖直平面内自由转动，定滑轮固定于地面上方L处，到O点的水平距离为
，电动机由跨过定滑轮且不可伸长的绳子与杆的中点相连，启动电动机，杆从虚线位置绕O点逆时针倒向地面，假设从
到
的过程中，杆做匀速转动(设杆与水平的夹角为α)，已知重力加速度为g，则在此过程中（ ）
A. 在前一半路程电动机对杆做的功比在后一半路程少
B. 电动机的输出功率先增大后减小
C. 杆对小球的作用力最大时，绳子对杆的拉力大小为4mg
D. 
时绳子对杆的拉力大小为mg
【答案】AC
【解析】在前一半程小球重力势能的减少量小于小球重力势能的减少量，根据功能关系，在前一半程电动机对杆做的功比在后一半程少，故选项A正确；电动机的输出功率一直在增大，故选项B错误；当α=0°时，杆对小球的作用力最大，此时绳子与水平面的夹角为30°，由力矩平衡可得，mg2L=FLsin30°，解得F=4mg．故选项C正确．当α=60°时，绳子对杆的拉力小于小球的重力mg，故选项D错误；故选AC．
练习册系列答案
阅读快车系列答案
相关题目
