题目内容
7.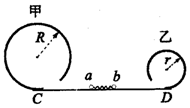 如图所示,半径分别为R和r(R>r)的甲、乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一光滑水平轨道CD相连,在水平轨道CD上有一轻弹簧被a、b两个小球夹住,但不拴接.同时释放两小球,a、b恰好分别通过甲、乙圆轨道的最高点.试求:
如图所示,半径分别为R和r(R>r)的甲、乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一光滑水平轨道CD相连,在水平轨道CD上有一轻弹簧被a、b两个小球夹住,但不拴接.同时释放两小球,a、b恰好分别通过甲、乙圆轨道的最高点.试求:(1)小球a通过圆轨道甲的最高点时的速度.
(2)己知小球a的质量为m,求小球b的质量.
(3)若ma=mb=m,且要求a、b都还能分别通过甲、乙圆轨道的最高点,则弹簧在释放前至少应具有多大的弹性势能?
分析 (1)两球均恰能通过最高点,这是一个临界状态,此刻球的速度最小,满足重力提供向心力,由此可求出到最高点的速度.
(2)释放弹簧前后,由于无机械能与其他能的转化,所以机械能守恒,动量守恒.由两个守恒列式能求出b球的质量.
(3)由能量守恒,弹簧具有的弹性势能就为两个球在最高点的机械能总和,由此可求出弹簧在释放前至少应具有多大的弹性势能.
解答 解:(1)小球在最高点受重力,弹力(方向均竖直向下),当小球a恰能通过圆轨道甲的最高点时,弹力为零,则有:$mg=m\frac{{v}_{a}{′}^{2}}{R}$
得:${v}_{a}′=\sqrt{gR}$
(2)同样道理,小球b通过圆轨道乙的最高点时,由${m}_{b}g={m}_{b}\frac{{v}_{b}{′}^{2}}{r}$得:${v}_{b}′=\sqrt{gr}$
设两小球离开 弹簧瞬间的速度分别为va、vb,由机械能守恒定律有:
$\frac{1}{2}m{{v}_{a}}^{2}=\frac{1}{2}m{v}_{a}{′}^{2}+mg•2R$
$\frac{1}{2}{m}_{b}{{v}_{b}}^{2}=\frac{1}{2}{m}_{b}{{v}_{b}′}^{2}+{m}_{b}g•2r$
解得:va=$\sqrt{5gR}$,vb=$\sqrt{5gr}$
又由动量守恒定律有:$m•\sqrt{5gR}={m}_{b}\sqrt{5gr}$
解得:mb=$\sqrt{\frac{R}{r}}m$
(3)当ma=mb=m时,Va=Vb,又由(1)(2)知,小球a能通过圆轨道甲的最高点,在刚离开弹簧时的速度条件为:${v}_{a}≥\sqrt{5gR}$,
故弹簧释放前至少具有的弹簧势能为:Ep=$2×\frac{1}{2}m(\sqrt{5gR})^{2}=5mgR$
答:(1)小球a通过圆轨道甲的最高点时的速度为$\sqrt{gR}$.
(2)己知小球a的质量为m,小球b的质量为$\sqrt{\frac{R}{r}}m$.
(3)若ma=mb=m,且要求a、b都还能分别通过甲、乙圆轨道的最高点,则弹簧在释放前至少应具有5mgR的弹性势能.
点评 本题考察的是动量守恒和机械能守恒的特殊情况,综合圆周运动向心力的临界状态.这里要注意的是不能把最高点的速度看成是零,这样的话小球到不了最高点时速度已经变为零了.

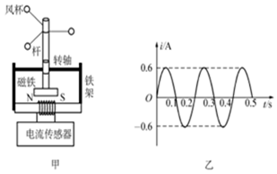
| A. | 此时电流的表达式为i=0.6sin10πt(A) | |
| B. | 此时电流的有效值为0.6$\sqrt{2}$A | |
| C. | 若风速变为2v1,此时传感器测得的电流随时间的变化为i=1.2sin10πt(A) | |
| D. | 若风速变为2v1,线圈中电流的有效值为0.6$\sqrt{2}$A |
 两个不规则带电导体间的电场线分布如图所示,已知导体附近的电场线均与导体表面垂直,a、b、c、d为电场中几个点,并且a、d为紧靠导体表面的两点,选无穷远为电势零点,则( )
两个不规则带电导体间的电场线分布如图所示,已知导体附近的电场线均与导体表面垂直,a、b、c、d为电场中几个点,并且a、d为紧靠导体表面的两点,选无穷远为电势零点,则( )| A. | 场强大小关系有Eb>Ec | |
| B. | 电势大小关系有φb<φd | |
| C. | 将一负电荷放在d点时其电势能为负值 | |
| D. | 将一正电荷由a点移到d点的过程中电场力做正功 |
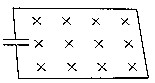 如图所示,在匀强磁场中,有一个接有电容器的导线回路,已知电容器电容C=30μF,回路面积为4×10-3m2,磁感应强度的变化规率为 B=0.5+5×10-2t(各物理量取国际单位制单位),则( )
如图所示,在匀强磁场中,有一个接有电容器的导线回路,已知电容器电容C=30μF,回路面积为4×10-3m2,磁感应强度的变化规率为 B=0.5+5×10-2t(各物理量取国际单位制单位),则( )| A. | 电容器上板带正电,电荷量为2×10-9C | |
| B. | 电容器上板带正电,电荷量为6×10-9C | |
| C. | 电容器上板带负电,电荷量为4×10-9C | |
| D. | 电容器上板带负电,电荷量为6×10-9C |
| A. | 太阳绕地球做匀速圆周运动 | |
| B. | 卡文迪许测量出了引力常量G的数值 | |
| C. | 牛顿发现了万有引力定律 | |
| D. | 托勒密提出了日心说 |
 在建筑工地上我们会见到如图所示的情形,运输民工用两手对称水平的用力将两长方体水泥制品夹紧并以加速度a竖直向上匀加速搬起,其中A的质量为3m,B的质量为m,水平作用力为F,A、B之间的动摩擦因数为μ,则在此过程中( )
在建筑工地上我们会见到如图所示的情形,运输民工用两手对称水平的用力将两长方体水泥制品夹紧并以加速度a竖直向上匀加速搬起,其中A的质量为3m,B的质量为m,水平作用力为F,A、B之间的动摩擦因数为μ,则在此过程中( )| A. | A、B所受到的合力方向都是竖直向上 | |
| B. | A、B之间的摩擦力大小为μF,A受到的摩擦力方向竖直向下 | |
| C. | A、B之间的摩擦力大小为m(g+a),A受到的摩擦力方向竖直向下 | |
| D. | A、B之间的摩擦力大小为m(g+a),A受到的摩擦力方向竖直向上 |

| A. | A、B两点的角速度比ωA:ωB=$\sqrt{3}$:1 | |
| B. | A、B两点的线速度比vA:vB=$\sqrt{3}$:1 | |
| C. | A、B两点的向心加速度比aA:aB=$\sqrt{3}$:1 | |
| D. | A、B两点的向心加速度方向都指向球心 |
 用频率为v0的光照射某种金属发生光电效应,测出光电流i随电压U的变化图象如图所示,该金属的极限频率v等于$\frac{h{v}_{0}-e{U}_{C}}{h}$,若照射到金属上的光子有a%被金属吸收,则这束光照射在金属表面上的功率P=$\frac{{I}_{0}h{v}_{0}}{ea%}$.(已知普朗克常量为h,电子的带电荷量为e).
用频率为v0的光照射某种金属发生光电效应,测出光电流i随电压U的变化图象如图所示,该金属的极限频率v等于$\frac{h{v}_{0}-e{U}_{C}}{h}$,若照射到金属上的光子有a%被金属吸收,则这束光照射在金属表面上的功率P=$\frac{{I}_{0}h{v}_{0}}{ea%}$.(已知普朗克常量为h,电子的带电荷量为e). 如图所示,有一长度为s=4m的斜面AB,斜面倾角θ=37°,斜面底端B与一绷紧的水平传送带的水平部分相距很近,传送带长度L=10m,并始终以v=2m/s的速率顺时针转动.一物体从斜面顶端A由静止释放,物体与斜面之间的动摩擦因数μ1=0.5,物体与传送带之间的动摩擦因数为μ2=0.1,已知物体从斜面底端B运动到传送带上的短暂过程,其速度大小不改变,将物体看作质点,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,有一长度为s=4m的斜面AB,斜面倾角θ=37°,斜面底端B与一绷紧的水平传送带的水平部分相距很近,传送带长度L=10m,并始终以v=2m/s的速率顺时针转动.一物体从斜面顶端A由静止释放,物体与斜面之间的动摩擦因数μ1=0.5,物体与传送带之间的动摩擦因数为μ2=0.1,已知物体从斜面底端B运动到传送带上的短暂过程,其速度大小不改变,将物体看作质点,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求: