��Ŀ����
����Ŀ����ͼ��ʾ����ֱ��Ϊ2R�İ�Բ�ε���̶�����ֱ���ڵ�A��B���㣬ֱ��AB����ֱ����ļн�Ϊ60�㣮�ڵ�������һ����Ϊm��СԲ����ԭ��Ϊ2R������ϵ��k= ![]() �ĵ�����������Բ���ҹ̶���A��B���㣮��֪��������������˶��ɣ����α���Ϊxʱ���е�������EP=
�ĵ�����������Բ���ҹ̶���A��B���㣮��֪��������������˶��ɣ����α���Ϊxʱ���е�������EP= ![]() kx2 �� �������ٶ�Ϊg������һ��Ħ������Բ����A�����·���C�㾲ֹ�ͷţ���Բ���˶����������͵�D��ʱ����
kx2 �� �������ٶ�Ϊg������һ��Ħ������Բ����A�����·���C�㾲ֹ�ͷţ���Բ���˶����������͵�D��ʱ����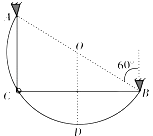
��1��Բ��������v��
��2�������Բ����������F�Ĵ�С��
���𰸡�
��1��
�⣺��ͼ��ʾ��

�ɼ���֪ʶ�ã�Բ����C�㡢D��ʱ���������α�����ͬ������������ȣ�
Բ����C��D�����У��ɻ�е���غ㶨�ɵã�mgh= ![]() mv2��
mv2��
�ɼ��ι�ϵ��֪��h= ![]() ��
��
��ã�v= ![]()
��2��
�⣺Բ����D��������ͼ���������ĵ�����
f=kx������x=�� ![]() ��1��R��
��1��R��
��D�㣬��ţ�ٵڶ����ɵã�
FN+fcos60��+fsin60�㩁mg=m ![]() ��
��
��ã�FN= ![]() mg
mg
����������1����C��D���̣��ɻ�е���غ㶨�ɿ������Բ�����ٶȣ���2��Բ����Բ���˶�����ţ�ٵڶ����ɿ��������D������Բ������������
�����㾫����ͨ��������û�е���ۺ�Ӧ�ã�����ϵͳ��̬���ܻ�е��E 1 ����ĩ̬���ܻ�е��E 2 ����E1 =E2��ϵͳ���ٵ����������ܦ�E P�� ����ϵͳ���ӵ��ܶ��ܦ�E K�� ������E P�� =��E K������ϵͳֻ��A��