��Ŀ����
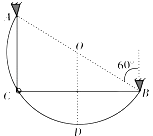
����Ŀ����ͼ��ʾ�����Ϊ37o�Ĵֲ�б��̶���ˮƽ�����ϣ�б���Ϸ���������Ϊ1kg��A��B�����壬A��B֮����һ����ϵ���ܴ�����ʵ��ɣ�������A˨������B�Ӵ�����˨������ʼ���ɱ���������������Ϊ4J��A��Bǡ�þ�ֹ��б���ϣ�������б�������Ħ�����뻬��Ħ������ȣ�B��б���Ķ�Ħ��������A��2�����ֽ������������A��B�ڼ��̵�ʱ���ڱ����ɵ�������
��1��A��B��б����Ħ������u1��u2�ֱ��Ƕ��٣�
��2�����ɸջָ�ԭ��ʱA��B���ٶȴ�Сv1��v2
��3�����ɸջָ�ԭ����1.2sʱ��A��B��ľ��룮
���𰸡�
��1��
�⣺A��Bǡ�þ�ֹ��б���ϣ�������ܵ���Ħ�����ĺ͵���������б�����µķ�����u1mgcos37��+u2mgcos37��=2mgsin37��
�֣�2u1=u2
�����ã�u1=0.5��u2=1
��2��
�⣺����A��B�ڼ��̵�ʱ���ڱ����ɵ�����������Ϊ�����ڷֿ��Ĺ�������б�淽��Ķ����غ㣬�ã�mv1=mv2
�֣�Ep= ![]() mv12+
mv12+ ![]() mv22
mv22
�����ã�v1=2m/s��v2=2m/s
��3��
�⣺A�����˶�ʱ��mgsin37��+u1mgcos37��=ma1
�ã�a1=10m/s2
�����˶���ʱ�䣺t1= ![]() s
s
���ϵ�λ�ƣ�x1= ![]() v1 t1=
v1 t1= ![]() =0.2m
=0.2m
A�����˶�ʱ��������Ϊ������mgsin37�㩁u1mgcos37��=ma2
�ã�a2=2m/s2
�˶���ʱ�䣺t2=1.2��t1=1s
�����˶���λ�ƣ�x2= ![]() a2t22=
a2t22= ![]() =1m
=1m
B�����˶�ʱ��mgsin37�㩁u2mgcos37��=ma
�ã�a=��2m/s2
t= ![]() =1s��1.2s
=1s��1.2s
x= ![]() =1m
=1m
����֮��ľ��룺��x=x����x2��x1��=1����1��0.2��=0.2m
����������1����ʼʱA��Bǡ�þ�ֹ��б���ϣ�����������������Ϲ�����ƽ������������������2�����ݶ����غ㣬��Ϲ��ܹ�ϵ�����������3���ֱ�����ǽ���������������ţ�ٵڶ�����������Եļ��ٶȣ�Ȼ�����˶�ѧ�Ĺ�ʽ���������

����Ŀ��ijͬѧ����ֱ���ҵ����ʵ����¼ӹҹ��룬̽�������뵯���쳤���Ĺ�ϵ���±��Ǹ�ͬѧ��ʵ�����ݣ�ʵ��ʱ����ʼ��δ���������ȣ�
��������m��10��3kg | 0 | 30 | 60 | 90 | 120 | 150 |
�����ܳ���l��10��2m | 6.0 | 7.2 | 8.4 | 9.6 | 10.8 | 12.0 |
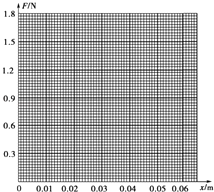
��1������ʵ������������ϵ����������F�������쳤��x��ϵ��ͼ�������ǵ�������������
��2������ͼ��õ����ɵľ���ϵ���� N/m�������������λ��Ч���֣�