Question

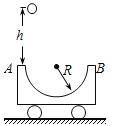
【题目】如图，半径为R、质量为2m的半圆轨道小车静止在光滑的水平地面上，将质量为m的小球(不计体积)从距A点正上方R高处由静止释放，小球自由落体后由A点经过半圆轨道后从B冲出，在空中能上升的最大高度为，则

A. 小球和小车组成的系统动量守恒

B. 小车向左运动的最大距离为2R/3

C. 小球离开小车后做竖直上抛运动

D. 小球第一次到最低点对半圆轨道的压力为7mg

Answer 1

【答案】BC

【解析】A、小球与小车组成的系统在水平方向所受合外力为零，水平方向系统动量守恒，但系统整体所受合外力不为零，系统动量不守恒，故A错误；

B、系统水平方向动量守恒，以向右为正方向，在水平方向，由动量守恒定律得：，，解得小车的位移：，故B正确；

C、小球与小车组成的系统在水平方向动量守恒，小球由A点离开小车时系统水平方向动量为零，小球与小车水平方向速度为零，小球离开小车后做竖直上抛运动，故C正确；

D、小球第一次在车中运动过程中，由动能定理得：，Wf为小球克服摩擦力做功大小，解得：，即小球第一次在车中滚动损失的机械能为，对称位置处速度变小，因此小车给小球的弹力变小，摩擦力变小，下降过程摩擦力做功大于于，机械能损失大于，根据动量守恒定律得：，根据能量守恒得，根据牛顿第二定律可得，联立解得，故D错误；

故选BC。