题目内容
【题目】如图甲所示，粒子源靠近水平极板M、N的M板，N板下方有一对长为L，间距为d=1.5L的竖直极板P、Q，再下方区域存在着垂直于纸面的匀强磁场，磁场上边界的部分放有感光胶片．水平极板M、N中间开有小孔，两小孔的连线为竖直极板P、Q的中线，与磁场上边界的交点为O．水平极板M、N之间的电压为U0；竖直极板P、Q之间的电压UPQ随时间t变化的图象如图乙所示；磁场的磁感强度B=
．粒子源连续释放初速不计、质量为m、带电量为+q的粒子，这些粒子经加速电场获得速度进入竖直极板P、Q之间的电场后再进入磁场区域，都会打到感光胶片上．已知粒子在偏转电场中运动的时间远小于电场变化的周期，粒子重力不计．求：
（1）带电粒子进入偏转电场时的动能EK；
（2）磁场上、下边界区域的最小宽度x；
（3）带电粒子打到磁场上边界感光胶片的落点范围．
【答案】（1）U0q．（2）L．（3）
．
【解析】（1）带电粒子进入偏转电场时的动能，即为MN间的电场力做的功EK=WMN=U0q
（2）设带电粒子以速度υ进入磁场，且与磁场边界之间的夹角为α时向下偏移的距离：△y=R-Rcosα=R（1-cosα）
而R＝
υ1=υsinα
△y＝
当α=90o时，△y有最大值．
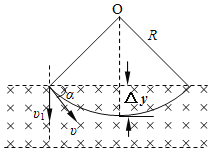
即加速后的带电粒子以υ1的速度进入竖直极板P、Q之间的电场不发生偏转，沿中心线进入磁场．磁场上、下边界区域的最小宽度即为此时的带电粒子运动轨道半径．
U0q＝
mυ12
所以
△ymax＝x＝
＝L
（3）粒子运动轨迹如图所示，若t=0时进入偏转电场，在电场中匀速直线运动进入磁场时R=L，打在感光胶片上距离中心线最近为x=2L
任意电压时出偏转电场时的速度为υn，根据几何关系
Rn＝
在胶片上落点长度为△x＝2Rncosα＝
打在感光胶片上的位置和射入磁场位置间的间距相等，与偏转电压无关．在感光胶片上的落点宽度等于粒子在电场中的偏转距离．带电粒子在电场中最大偏转距离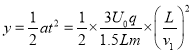
粒子在感光胶片上落点距交点O的长度分别是2L和
，则落点范围是
．
