Question

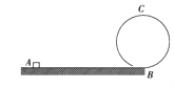
【题目】如图所示，一个小物块静止在水平轨道上的A点，水平轨道右侧与一竖直光滑圆轨道平滑连接于B点，小物块可不受阻碍地进入圆轨道，C为圆轨道的最高点。在极短时间内给小物块一水平向右的冲量I，使小物块从A点向右运动。已知小物块的质量m=2kg，小物块与水平轨道间的动摩擦因数μ=0.4，圆轨道的半径R=0.24m，A、B两点的距离L=0.5m，重力加速度g=10m/s2，问：

(1)冲量I为多大时，小物块恰好运动到B点

(2)冲量I为多大时，小物块能顺利经过圆轨道的C点

Answer 1

【答案】(1)；(2)

【解析】

(1)设小物块的初速度为，则由动量定理得

对小物块恰能到达B点的过程应用动能定理得：

联立解得

(2)设小物块恰能通过C点时的速度为,由向心力公式得

对小物块从A到C过程,由动能定理得：

联立以上各式得

即冲量,小物块能顺利经过圆轨道的C点。