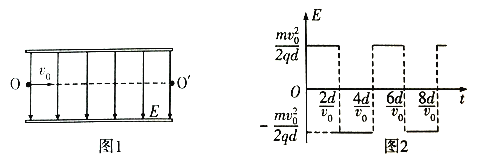
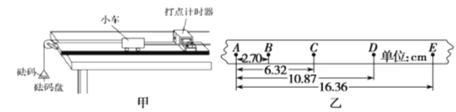
��Ŀ����
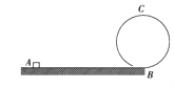
����Ŀ����ͼ��ʾ��һ����m=lkg�ij�ľ�徲ֹ�ڹ⻬��ˮƽ���ϣ�һ������M=2kg����飨����Ϊ�ʵ㣩���ڳ�ľ�����ˡ���ľ�����Ҳ���ֱ�����㹻Զ����ͬʱ�����ˮƽ���ҡ�����ľ��ˮƽ�����Ҵ�С��Ϊ![]() =2m/s�ij��ٶȣ���֪����볤ľ���Ķ�Ħ������
=2m/s�ij��ٶȣ���֪����볤ľ���Ķ�Ħ������![]() ����ľ���뵲����ײʱ�伫������ײ��������е����ʧ�����ʼ��û�дӳ�ľ���ϵ��������������ٶ�g=10m/s2����
����ľ���뵲����ײʱ�伫������ײ��������е����ʧ�����ʼ��û�дӳ�ľ���ϵ��������������ٶ�g=10m/s2����
(1)��ľ�峤�ȵ���СֵL��
(2)����볤ľ�忪ʼ�˶�����ľ���n������ֱ������ײǰ�Ĺ����У������Գ�ľ�廬������ʱ��t��
![]()
���𰸡�(1)![]() ��(2)
��(2)![]()
��������
(1)������֪����ľ���뵲��ÿ����ײǰ����볤ľ���Ѵﹲͬ�ٶȣ���ľ������ֱ��������ײ��ͣ�ڵ��崦������ľ��ij�����Сʱ���ͣ�ڳ�ľ����Ҷˣ������������������غ㶨����
![]()
���
![]()
(2)�賤ľ�����Ҳ൲���һ����ײǰ������볤ľ��Ĺ�ͬ�ٶ�Ϊ![]() ���ɶ����غ㶨�ɵ�
���ɶ����غ㶨�ɵ�
![]()
���
![]()
��һ����ײǰ�����Գ�ľ�廬����ʱ��
![]()
��ľ���뵲��ڶ�����ײǰ��������볤ľ��Ĺ�ͬ�ٶ�Ϊ![]() ���ɶ����غ㶨�ɵ�
���ɶ����غ㶨�ɵ�
![]()
���
![]()
��һ����ײ����ڶ�����ײǰ�����Գ�ľ�廬����ʱ��
![]()
��ľ���뵲���������ǰ��������볤ľ��Ĺ�ͬ�ٶ�Ϊ![]() ���ɶ����غ㶨�ɵ�
���ɶ����غ㶨�ɵ�
![]()
���
![]()
�ڶ�����ײ�����������ײǰ�����Գ�ľ�廬����ʱ��
![]()
����
�������ƣ�����볤ľ�忪ʼ�˶�����ľ���n������ֱ������ײǰ�Ĺ����У������Գ�ľ�廬������ʱ��Ϊ
![]()