题目内容
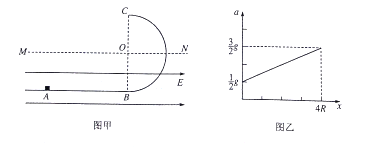
【题目】2014年2月8日第22届冬季奥林匹克运动会在俄罗斯联邦索契市胜利开幕，设一个质量m=50kg的跳台花样滑雪运动员（可看成质点），从静止开始沿斜面雪道从A点滑下，沿切线从B点进入半径R=15m的光滑竖直冰面圆轨道BPC，通过轨道最高点C水平飞出，经t=2s落到斜面雪道上的D点，其速度方向与斜面垂直，斜面与水平面的夹角
=37°，运动员与雪道之间的动摩擦因数
=0．075，不计空气阻力，取当地的重力加速度g=l0m/s2，（ sin37°=0．60，cos37°=0．80）。试求：
（1）运动员运动到C点时的速度大小VC;
（2）运动员在圆轨道最低点P受到轨道支持力的大小FN；
（3）A点离过P点的水平地面的高度h；
【答案】（1）15m/s（2）3250N（3）45.5m
【解析】（1）运动员从C点到D点做平抛运动，在D点对速度进行分解，
根据运动的分解得：得： 
，代入数据解得
（2）设运动员运动到P点时的速度大小为
，根据机械能守恒定律得： 
，
根据牛顿第二定律得
，联立解得
（3）根据动能定理研究从A点到P点有
联立解得： 
新活力总动员暑系列答案
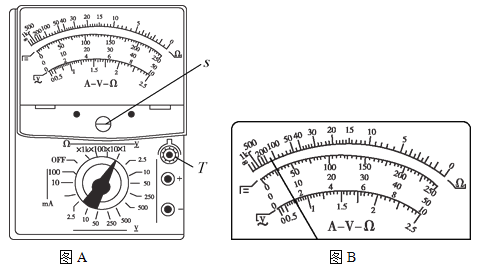
龙人图书快乐假期暑假作业郑州大学出版社系列答案
【题目】某兴趣小组设计了一个寻求碰撞前后不变量的实验。实验器材有：打点计时器、低压交流电源(f=50Hz)、纸带、刻度尺、表面光滑的平直金属轨道、带撞针的小车甲、带橡皮泥的小车乙、天平。
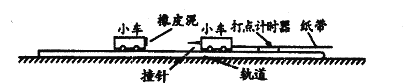
该小组实验的主要步骤有：
A用天平测出甲的质量m甲=0.50kg，乙的质量m乙=0.25kg
B．更换纸带重复操作三次
C．接通电源，并给甲车一定的初速度v甲
D．将平直轨道放在水平桌面上，在其一端固定打点计时器，连接电源
E．将小车甲靠近打点计时器放置，在车后固定纸带，将小车乙静止地放在平直轨道中间位置
(1)上述实验步骤合理的顺序为A_________，（补充完整）
(2)从打下的纸带中，选取比较理想的一条，如下图所示，请补充完成下表（均保留两位有效数字）
| 甲车 | 乙车 | 甲乙整体 |
m/kg | 0.50 | 0.25 | 0.75 |
v/(m/s) | 3.0 | 0 | ______ |
| 6.0 | 0 | 2.7 |
mv | 1.5 | 0 | ______ |
mv2 | 4.5 | 0 | 3.0 |
(3)根据以上数据寻找出碰撞前后不变量的表达式为_____________________.
