题目内容
12．在外界气压为1标准大气压的状况下，将半径为0.1m的两个马德堡半球合拢，抽去里面一部分空气，使得球内部气体的压强降为0.5个标准大气压，估算大约需要用力500πN 才能将两半球拉开；未拉开时两半球密封处每1cm 长度受到的挤压力的大小约为25πN．分析 要想将两半球拉开，需要克服大气压力，根据F=PS可求出大气压力的大小从而求得拉力．
解答 解：马德堡半球的有效受力面积为：S=πR2=π（0.1）2=0.01π
内外压强差为：p=0.5×1.0×105pa=5.0×104pa
半球受到的压力为：F=p×s=5.0×104pa×0.01π=500πN．
直径为2r=0.2m=20cm，所以两半球密封处每1cm长度受到的挤压力的大小约为：F′=$\frac{F}{20}$=$\frac{500π}{20}$=25πN
故答案为：500π；25π．
点评 本题考查了学生对大气压强的认识和理解，并可以利用F=PS求解压力，本题难度不大，是一道基础题．
练习册系列答案
相关题目
2．
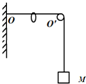如图所示，一不可伸长的光滑轻绳，其左端固定于O点，右端跨过位于O′点的固定光滑轴悬挂质量为M的物体，OO′段水平且长为L，绳上套一光滑的轻环．若在轻环上施加竖直向下的作用力F，物体上升L后再次达到平衡，此时F大小（ ）
如图所示，一不可伸长的光滑轻绳，其左端固定于O点，右端跨过位于O′点的固定光滑轴悬挂质量为M的物体，OO′段水平且长为L，绳上套一光滑的轻环．若在轻环上施加竖直向下的作用力F，物体上升L后再次达到平衡，此时F大小（ ）| A． | $\frac{\sqrt{2}}{2}$Mg | B． | $\frac{\sqrt{3}}{2}$Mg | C． | $\sqrt{2}$Mg | D． | $\sqrt{3}$Mg |
质量为M的轮轴其轴半径为r，轮半径为R，可绕水平转轴O转动，重物质量为m，由轻绳绕在轮轴上，如图所示，重物由静止下落高度h时的速度为v，则此时轮边缘某点的线速度为$\frac{Rv}{r}$；轮轴转动的动能为$mgh-\frac{1}{2}m{v^2}$（不计一切阻力）．
7．如图所示，ABCD是一段竖直平面内的光滑轨道，AB段与水平面成α角，CD段与水平面成β角，其中BC段水平，且其长度大于L．现有两小球P、Q，质量分别是3m、2m，用一长为L的轻质直杆连接，将P、Q由静止从高H处释放，在轨道转折处用光滑小圆弧连接，不考虑两小球在轨道转折处的能量损失，则小球P滑上CD轨道的最大高度h为（ ）
| A． | h=H | B． | h=H+Lsinβ | ||
| C． | h=H+$\frac{L（sinα-sinβ）}{5}$ | D． | h=H+$\frac{L（3sinα-2sinβ）}{5}$ |
如图所示，两端开口、粗细均匀的足够长玻璃管插在大水银槽中，管的顶部有一定长度的水银．两段空气柱被封闭在左右两侧的竖直管中．开启顶部连通左右水银的阀门，右侧空气柱长为L0，右侧空气柱底部水银面比槽中水银面高出h，右侧空气柱顶部水银面比左侧空气柱顶部水银面低h．
如图，导热性能良好的气缸放置在水平平台上，活塞质量m=10kg，横截面积S=50cm2，大气压强为p0=l×105Pa，当温度为t1=-3℃时，活塞封闭的气柱长L1=10cm．将气缸倒过来放置，活塞下方的空气能通过平台上的缺口与大气相通，缓慢升高周围的温度到多少摄氏度时，封闭气柱的长为L2=18cm．g取l0m/s2，气缸足够长．
4．如图甲所示，物体以一定的初速度从倾角α=37°的斜面底端沿斜面向上运动，上升的最大高度为3.0m．选择地面为参考平面，上升过程中，物体的机械能E随高度h的变化图象如图乙所示．g=10m/s2，sin37°=0.60，cos37°=0.80．则（ ）
| A． | 物体上升过程的加速度大小a=10m/s2 | |
| B． | 物体与斜面间的动摩擦因数μ=0.40 | |
| C． | 物体的质量m=0.67kg | |
| D． | 物体回到斜面底端时的动能Ek=10J |