题目内容
2．
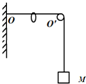如图所示，一不可伸长的光滑轻绳，其左端固定于O点，右端跨过位于O′点的固定光滑轴悬挂质量为M的物体，OO′段水平且长为L，绳上套一光滑的轻环．若在轻环上施加竖直向下的作用力F，物体上升L后再次达到平衡，此时F大小（ ）| A． | $\frac{\sqrt{2}}{2}$Mg | B． | $\frac{\sqrt{3}}{2}$Mg | C． | $\sqrt{2}$Mg | D． | $\sqrt{3}$Mg |
分析 由几何关系求出环两边绳子的夹角，然后根据平行四边形定则求F．
解答 解：重新平衡后，绳子形状如下图：
由几何关系知：绳子与竖直方向夹角为30°，则环两边绳子的夹角为60°，则根据平行四边形定则，环两边绳子拉力的合力为$\sqrt{3}$Mg，
根据平衡条件，F=$\sqrt{3}$Mg
故选：D
点评 该题的关键在于能够对线圈进行受力分析，利用平衡状态条件解决问题．力的计算离不开几何关系和三角函数．
练习册系列答案
培优三好生系列答案
相关题目
13．
某物体在水平拉力作用下沿着粗糙的水平面做直线运动，运动的速度随时间变化的规律如图示．下列结论不正确的是（ ）
某物体在水平拉力作用下沿着粗糙的水平面做直线运动，运动的速度随时间变化的规律如图示．下列结论不正确的是（ ）| A． | 在0～t0时间内加速度不变，在t0～3t0时间内加速度减小 | |
| B． | t0时刻物体的位移最大 | |
| C． | 在t0～3t0的时间内，平均速度小于$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D． | t0～3t0，所受的拉力越来越大 |
10．如图所示，水平桌面上物体P绕中心O点做匀速圆周运动，下列说法正确的是（ ）
| A． | P做变加速运动 | |
| B． | P处于平衡状态 | |
| C． | P所受的合力是零 | |
| D． | P的向心加速度方向与速度方向一致 |
某探究学习小组的同学欲验证动能定理，他们在实验室组装了一套如图所示的装置，另外他们还找到了打点计时器所用的学生电源、导线、复写纸、纸带、滑块、细砂．若你是小组中的一位成员，要完成该项实验，则：
7．
t=0时刻质点位于x=-2m处，沿x轴正向做直线运动，其运动的v-t图象如图所示．下列说法正确的是（ ）
t=0时刻质点位于x=-2m处，沿x轴正向做直线运动，其运动的v-t图象如图所示．下列说法正确的是（ ）| A． | t=4 s时，质点在x=1m处 | |
| B． | 第3s内和第4s内，质点加速度的方向相反 | |
| C． | 第3s内和第4s内，质点加速度的方向相同 | |
| D． | 0～2 s内和0～4 s内，质点的平均速度相同 |
14．用手握住瓶子，使瓶子在竖直方向静止，如果握力加倍，则手对瓶子的摩擦力（ ）
| A． | 握力越大，摩擦力越大 | B． | 只要瓶子不动，摩擦力大小不变 | ||
| C． | 方向由向下变成向上 | D． | 手越粗糙，摩擦力越大 |
11．
如图所示，电源电动势为E，内阻为r，R1＞r，当电路中滑动变阻器R2的滑动触头P向上滑动时，以下说法正确的是（ ）
如图所示，电源电动势为E，内阻为r，R1＞r，当电路中滑动变阻器R2的滑动触头P向上滑动时，以下说法正确的是（ ）| A． | 电容器的带电量增大 | B． | 电压表的读数变大 | ||
| C． | 电源的总功率（整个电路的功率）变大 | D． | 电源的输出功率变小 |