题目内容
3. 质量为M的轮轴其轴半径为r,轮半径为R,可绕水平转轴O转动,重物质量为m,由轻绳绕在轮轴上,如图所示,重物由静止下落高度h时的速度为v,则此时轮边缘某点的线速度为$\frac{Rv}{r}$;轮轴转动的动能为$mgh-\frac{1}{2}m{v^2}$(不计一切阻力).
质量为M的轮轴其轴半径为r,轮半径为R,可绕水平转轴O转动,重物质量为m,由轻绳绕在轮轴上,如图所示,重物由静止下落高度h时的速度为v,则此时轮边缘某点的线速度为$\frac{Rv}{r}$;轮轴转动的动能为$mgh-\frac{1}{2}m{v^2}$(不计一切阻力).
分析 同轴转动,角速度相等,根据公式v=ωr求解轮边缘某点的线速度.根据系统的机械能守恒定律求解轮轴转动的动能.
解答 解:轮轴转动的角速度为:ω=$\frac{v}{r}$;
故轮边缘某点的线速度为:v′=ωR=$\frac{Rv}{r}$;
根据重物和轮轴组成的系统机械能守恒得:
轮轴转动的动能为:Ek=mgh-$\frac{1}{2}m{v}^{2}$;
故答案为:$\frac{Rv}{r}$,$mgh-\frac{1}{2}m{v^2}$.
点评 本题关键明确共轴转动的物体角速度相等,整个系统机械能守恒,同时结合公式v=ωr列式求解.

练习册系列答案
相关题目
13. 某物体在水平拉力作用下沿着粗糙的水平面做直线运动,运动的速度随时间变化的规律如图示.下列结论不正确的是( )
某物体在水平拉力作用下沿着粗糙的水平面做直线运动,运动的速度随时间变化的规律如图示.下列结论不正确的是( )
 某物体在水平拉力作用下沿着粗糙的水平面做直线运动,运动的速度随时间变化的规律如图示.下列结论不正确的是( )
某物体在水平拉力作用下沿着粗糙的水平面做直线运动,运动的速度随时间变化的规律如图示.下列结论不正确的是( )| A. | 在0~t0时间内加速度不变,在t0~3t0时间内加速度减小 | |
| B. | t0时刻物体的位移最大 | |
| C. | 在t0~3t0的时间内,平均速度小于$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D. | t0~3t0,所受的拉力越来越大 |
14.用手握住瓶子,使瓶子在竖直方向静止,如果握力加倍,则手对瓶子的摩擦力( )
| A. | 握力越大,摩擦力越大 | B. | 只要瓶子不动,摩擦力大小不变 | ||
| C. | 方向由向下变成向上 | D. | 手越粗糙,摩擦力越大 |
11. 如图所示,电源电动势为E,内阻为r,R1>r,当电路中滑动变阻器R2的滑动触头P向上滑动时,以下说法正确的是( )
如图所示,电源电动势为E,内阻为r,R1>r,当电路中滑动变阻器R2的滑动触头P向上滑动时,以下说法正确的是( )
 如图所示,电源电动势为E,内阻为r,R1>r,当电路中滑动变阻器R2的滑动触头P向上滑动时,以下说法正确的是( )
如图所示,电源电动势为E,内阻为r,R1>r,当电路中滑动变阻器R2的滑动触头P向上滑动时,以下说法正确的是( )| A. | 电容器的带电量增大 | B. | 电压表的读数变大 | ||
| C. | 电源的总功率(整个电路的功率)变大 | D. | 电源的输出功率变小 |
18.天然放射性元素${\;}_{90}^{232}$Th(钍)经过一系列α衰变和β衰变之后,变成${\;}_{82}^{208}$Pb(铅),下列论断中正确的是( )
| A. | 铅核比钍核少24个中子 | |
| B. | 衰变过程中共有6次α衰变和4次β衰变 | |
| C. | 铅核比钍核少8个质子 | |
| D. | 衰变过程中共有4次α衰变和8次β衰变 |
8.关于密封容器中气体压强产生的原因,下列说法正确的是( )
| A. | 是由于气体分子间的相互作用力(引力和斥力)而产生的 | |
| B. | 是容器壁对气体分子的排斥而产生的 | |
| C. | 是大量气体分子频繁地碰撞器壁而产生的 | |
| D. | 是由于气体受到重力作用而产生的 |
15. 如图所示,固定的水平长直导线中通有电流I,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )
如图所示,固定的水平长直导线中通有电流I,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )
 如图所示,固定的水平长直导线中通有电流I,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )
如图所示,固定的水平长直导线中通有电流I,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )| A. | 穿过线框的磁通量保持不变 | B. | 线框中感应电流方向为逆时针 | ||
| C. | 线框所受安培力的合力为零 | D. | 线框的机械能不断减少 |
15.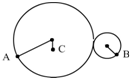 如图所示的装置中,已知大齿轮的半径是小齿轮的3倍,A点和B点分别在两轮边缘,C点离大轮轴距离等于小轮半径,若不打滑,则他们的线速度之比VA:VB:VC为( )
如图所示的装置中,已知大齿轮的半径是小齿轮的3倍,A点和B点分别在两轮边缘,C点离大轮轴距离等于小轮半径,若不打滑,则他们的线速度之比VA:VB:VC为( )
 如图所示的装置中,已知大齿轮的半径是小齿轮的3倍,A点和B点分别在两轮边缘,C点离大轮轴距离等于小轮半径,若不打滑,则他们的线速度之比VA:VB:VC为( )
如图所示的装置中,已知大齿轮的半径是小齿轮的3倍,A点和B点分别在两轮边缘,C点离大轮轴距离等于小轮半径,若不打滑,则他们的线速度之比VA:VB:VC为( )| A. | 9:3:1 | B. | 1:3:3 | C. | 3:3:1 | D. | 3:9:1 |