题目内容
17.如图1所示,在水平放置,内壁光滑,面积不等的气缸里,活塞A的面积SA=10cm2,活塞B的面积SB=20cm2,两活塞用质量不计的细绳连接,活塞A还通过细绳、定滑轮与重物C相连,在缸内气温t1=227℃,压强p1=1.1×105Pa时,两活塞保持静止,此时两活塞离开气缸接缝处距离都是L=10cm,大气压强p0=1.0×105 Pa保持不变,试求: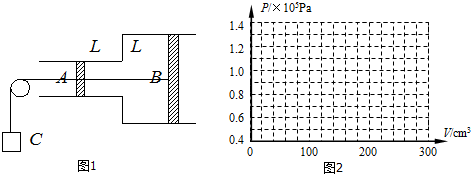
(1)重物C的质量M;
(2)当活塞A、B间细绳拉力为零时,气缸内气体的温度;
(3)若温度由t1缓慢下降到-23℃,试在P-V图上(图2)画出气缸内气体状态的变化的图线.
分析 (1)取两活塞整体研究,根据平衡条件求解.
(2)找出变化的初末状态,根据理想气体方程$\frac{pV}{T}$=C求解.
(3)封闭气体先作等压变化,活塞一起向左移动,直到B被卡住.接着体积保持不变,压强减小,直到A被拉动.最后气体作等压变化.分别根据气态方程求出温度,再作出图线
解答 解:(1)对两活塞组成的系统,由平衡条件得:
Mg+p1SA+p0SB=p0SA+p1SB,其中:p1=p0+$\frac{Mg}{{S}_{B}-{S}_{A}}$,代入数据解得:M=1kg;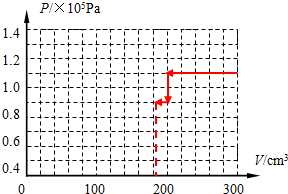
(2)当活塞A、B间细绳拉力为零时,气体的压强为:p2=p0-$\frac{Mg}{{S}_{A}}$=0.9×105Pa,
根据理想气体状态方程得:$\frac{{p}_{1}{V}_{1}}{{T}_{1}}$=$\frac{{p}_{2}{V}_{2}}{{T}_{1}}$,代入数据解得:T2=272.7K,则:t2=-0.3℃;
(3)先等压,体积减小,活塞一起左移,直到B被卡住,$\frac{300}{273+227}=\frac{200}{273+t}$,t=60.3?C
再体积不变,压强减小,到A被推动,$\frac{{1.1×{{10}^5}}}{273+60.3}=\frac{{0.9×{{10}^5}}}{273+t'}$,t’=-0.3°C
再等压体积减小,$\frac{200}{273-0.3}=\frac{V}{273-23}$,V=183.3cm3,图象如图所示:
答:(1)重物C的质量M为1kg;
(2)当活塞A、B间细绳拉力为零时,气缸内气体的温度为-0.3℃;
(3气缸内气体状态的变化的图线如图所示.
点评 本题的解题关键是分析气体作何种变化.根据力学知识求封闭气体的压强,根据气体的状态变化过程,选择相应的实验定律都是应具备的解题能力.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 t=0时刻质点位于x=-2m处,沿x轴正向做直线运动,其运动的v-t图象如图所示.下列说法正确的是( )
t=0时刻质点位于x=-2m处,沿x轴正向做直线运动,其运动的v-t图象如图所示.下列说法正确的是( )| A. | t=4 s时,质点在x=1m处 | |
| B. | 第3s内和第4s内,质点加速度的方向相反 | |
| C. | 第3s内和第4s内,质点加速度的方向相同 | |
| D. | 0~2 s内和0~4 s内,质点的平均速度相同 |
| A. | 是由于气体分子间的相互作用力(引力和斥力)而产生的 | |
| B. | 是容器壁对气体分子的排斥而产生的 | |
| C. | 是大量气体分子频繁地碰撞器壁而产生的 | |
| D. | 是由于气体受到重力作用而产生的 |
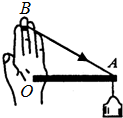 如图所示,用一根细绳和一根轻直杆组成三角支架,绳的一端绕在手指上B点,杆的一端顶在掌心O处,当在A处挂上重物时,整个系统处于静止状态,此时杆OA处于水平状态,绳与杆分别对手指和手掌有力的作用,对这两个作用力的说法正确的是( )
如图所示,用一根细绳和一根轻直杆组成三角支架,绳的一端绕在手指上B点,杆的一端顶在掌心O处,当在A处挂上重物时,整个系统处于静止状态,此时杆OA处于水平状态,绳与杆分别对手指和手掌有力的作用,对这两个作用力的说法正确的是( )| A. | 绳对手指的拉力沿AB方向(与图示方向相反) | |
| B. | 杆对手掌的拉力沿OA方向 | |
| C. | 绳子对A点的作用力和杆对A点的作用力的合力大小大于重物的重力 | |
| D. | 绳子对A点的作用力和杆对A点的作用力的合力方向竖直向上 |
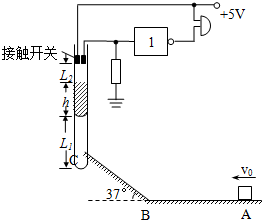 如图所示为一简易火灾报警装置.其原理是:开口向上竖直放置的试管中装有水银,内有接触开关(厚度不计),只要有水银浸没,它就会导通,蜂鸣器发出报警的响声.27℃时,空气柱长度L1为30cm,水银上表面与接触开关下端的距离L2为10cm,管内水银柱的高度h为25cm,外界大气压强为75cmHg.求:
如图所示为一简易火灾报警装置.其原理是:开口向上竖直放置的试管中装有水银,内有接触开关(厚度不计),只要有水银浸没,它就会导通,蜂鸣器发出报警的响声.27℃时,空气柱长度L1为30cm,水银上表面与接触开关下端的距离L2为10cm,管内水银柱的高度h为25cm,外界大气压强为75cmHg.求: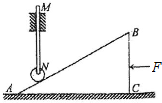 有一重力为2000N的竖直杆MN限制在如图所示的卡槽中,只能沿竖直方向运动,它跨斜面接触端装一轻质滑轮,斜面AB长5m,高BC长3m,在BC边加一水平推力F使斜面体沿水平方向匀速运动(不考虑一切摩擦).求推力F的大小是多少?
有一重力为2000N的竖直杆MN限制在如图所示的卡槽中,只能沿竖直方向运动,它跨斜面接触端装一轻质滑轮,斜面AB长5m,高BC长3m,在BC边加一水平推力F使斜面体沿水平方向匀速运动(不考虑一切摩擦).求推力F的大小是多少? 如图所示,在倾角为θ的固定光滑绝缘斜面上,有一劲度系数为k的长绝缘轻质弹簧,其下端固定于斜面底端,上端与一质量为m,带正电的小球A相连,整个空间存在一平行于斜面向上的匀强磁场,小球A静止时弹簧恰为原长.另一质量也为m的不带电的绝缘小球B从斜面上的P点由静止开始下滑,与A发生碰撞后一起沿斜面向下运动,碰撞时间极短,且不粘连.在以后的运动过程中,A与B左所能达到的最高点恰未分开.全过程中小球A的电量不发生变化,弹簧形变始终在弹性限度内,重力加速度为g.求:
如图所示,在倾角为θ的固定光滑绝缘斜面上,有一劲度系数为k的长绝缘轻质弹簧,其下端固定于斜面底端,上端与一质量为m,带正电的小球A相连,整个空间存在一平行于斜面向上的匀强磁场,小球A静止时弹簧恰为原长.另一质量也为m的不带电的绝缘小球B从斜面上的P点由静止开始下滑,与A发生碰撞后一起沿斜面向下运动,碰撞时间极短,且不粘连.在以后的运动过程中,A与B左所能达到的最高点恰未分开.全过程中小球A的电量不发生变化,弹簧形变始终在弹性限度内,重力加速度为g.求: