Question

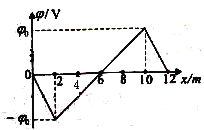
【题目】离子推进器是太空飞行器常用的动力系统．某种推进器设计的简化原理如图所示，截面半径为 R=2m的圆柱腔分为两个工作区．Ⅰ为电离区，电离区间充有稀薄铯气体，也有轴向的匀强磁场，磁感应强度大小为，在离轴线 R/2 处的 C点持续射出一定速率范围的电子．假设射出的电子仅在垂直于轴线的截面上运动，截面如图2 所示(从左向右看)．电子的初速度方向与中心 O 点和 C 点的连线成 ()．电子碰撞铯原子使之电离，为了取得好的电离效果，从内圆柱体表面发出的电子在区域内运动时不能与外器壁碰撞。Ⅱ为加速区，两端加有电压，形成轴向的匀强电场．Ⅰ区产生的铯离子以接近 0 的初速度进入Ⅱ区，被加速后以速度从右侧喷出．这种高速粒子流喷射出去，可推动卫星运动，电子在Ⅰ区内不与器壁相碰且能到达的区域越大，电离效果越好，已知铯离子荷质比，铯离子，电子质量为，电量为， (电子碰到器壁即被吸收，不考虑电子间的碰撞)。

（1）求Ⅱ区的加速电压；

（2）为取得好的电离效果，请判断Ⅰ区中的磁场方向(按图 2 说明是“垂直纸面向里”或“垂直纸面向外”)；

（3）要取得好的电离效果，求射出的电子最大速率与角的关系；

（4）若单位时间内喷射出个铯离子，试求推进器的推力(结果取两位有效数字)。

Answer 1

【答案】（1）（2）垂直纸面向外(3) (4)

【解析】试题分析：（1）粒子在区域Ⅱ中运动的过程中，只受电场力作用，电场力做正功，利用动能定可解的加速电压．（2）因电子在I区内不与器壁相碰且能到达的区域越大，电离效果越好，所以可知电子应为逆时针转动，结合左手定则可知磁场的方向．（3）画出轨迹图，通过几何关系解出轨道的最大半径，再结合洛伦兹力提供向心力列式，即可得出射出的电子最大速率与的关系．（4）根据动量定理即可求解推进器的推力.

（1）带电粒子在II区加速，根据动能定理得： ，解得：

（2）要取得较好的电离效果，电子须在出射方向左边做匀速圆周运动，即为按逆时针方向旋转，根据左手定则可知，此刻Ⅰ区磁场应该是垂直纸面向外．

（3）当电子以角入射时，最大速度对应轨迹如图所示

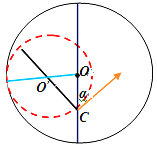
轨迹圆与圆柱腔相切，此时有： ， ，

由余弦定理得： ，又

联立解得：

在磁场中有：

联立解得：

（4）根据动量定理得：

代入数据得：