题目内容
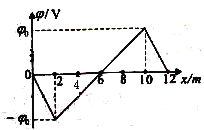
【题目】有一沿x轴方向的静电场，其电势φ随x轴坐标的变化情况如图所示。P、Q为x轴上的两点，其坐标分别为
=lcm、
=4cm。若将一质量为m、电荷量为q的带正电粒子(重力不计)从x轴上的某处释放，则下列说法中正确的是( )
A. 若该粒子从坐标原点处由静止释放，则粒子在P点和Q点的加速度大小相等，方向相反
B. 若该粒子从坐标原点处由静止释放，则粒子经过P点和Q点时，电场力做功的功率相等
C. 若该粒子从Q点由静止释放，则粒子将沿x轴负方向一直向前运动
D. 若该粒子从P点以沿x轴正方向的水平速度
释放，则粒子将沿x轴正方向一直向前运动
【答案】D
【解析】A、φ-x图象的斜率大小等于场强E．则知P点的场强大于Q点的场强，根据牛顿第二定律
知粒子在P点的加速度大于在Q点的加速度，加速度方向相反，故A错误。B、粒子经过P点与Q点时电势相等则电势能相等有动能相等，速度大小相等；由图象知道电场强度之比为2：1，所以电场力大小之比为2：1，根据P=Fv，电场力做功的功率大小是Q点的两倍，B错误。C、若粒子从Q点释放，先向x轴负方向加速运动再减速运动，到达P点时速度减为零，此时电场力沿x轴正向，故反向做加速运动，C错误。D、粒子在P点以某一初速度释放,先加速后减速运动到Q点速度相等，假设此后减速过程到10mm处速度减为零时电场力做的负功为
，解得
，则保证运动不反向的初速度至少为
,D正确.故选D.
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
