题目内容
5. 如图所示,倾角θ=30°、长L=2.7m的斜面,底端与一个光滑的$\frac{1}{4}$圆弧平滑连接,圆弧底端切线水平.一个质量为m=1kg的质点从斜面最高点A沿斜面由静止下滑,经过斜面底端B恰好到达圆弧最高点C,又从圆弧滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧上升,再滑回,这样往复运动,最后停在B点.已知质点与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,g=10m/s2.假设质点经过斜面与圆弧平滑连接处速率不变.求:
如图所示,倾角θ=30°、长L=2.7m的斜面,底端与一个光滑的$\frac{1}{4}$圆弧平滑连接,圆弧底端切线水平.一个质量为m=1kg的质点从斜面最高点A沿斜面由静止下滑,经过斜面底端B恰好到达圆弧最高点C,又从圆弧滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧上升,再滑回,这样往复运动,最后停在B点.已知质点与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,g=10m/s2.假设质点经过斜面与圆弧平滑连接处速率不变.求:(1)质点第1次经过B点时对圆弧轨道的压力;
(2)质点从A到D的过程中质点下降的高度;
(3)质点从开始到最后停止运动的过程中在斜面上滑过的路程;
(4)质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量.
分析 (1)根据动能定理求出质点第1次到达B点的速度,结合牛顿第二定律和第三定律求出质点对圆弧轨道的压力.
(2)对AB段和BD段分别运用动能定理,求出BD的长度,从而得出质点从A到D的过程中质点下降的高度.
(3)整个过程中,摩擦力做功即为机械能的减少量,当最终停在B点时求出机械能的减少量,根据摩擦力做功求出运动路程
(4)分别对上滑过程和下滑过程运用动能定理,得出上滑的位移与下滑的位移的关系,从而找出规律,得出质点在斜面上运动的路程,通过Q=fs求出产生的热量
解答 解:(1)设圆弧的半径为R,则质点从C到B过程,有:
mgR=$\frac{1}{2}m{v}^{2}$
FN-mg=m$\frac{{v}^{2}}{R}$
得:FN=3mg=3×1×10N=30N
根据牛顿第三定律,质点第1次经过B点对圆弧轨道的压力为30N.
(2)设AD高度为h,选A经B到C再返回D的过程,根据动能定理知
mgh-μmgcos30°(2L-$\frac{h}{sin30°}$)=0
解得:h=0.9m
则质点从A点到D点下降的高度为:h=0.9m
AD的距离为:L1=L-2h=0.9m
(3)当最终停在B点时,机械能减少量为:△Ep=mgLsin30°=1×10×2.7×0.5=13.5J
滑块在斜面上所受摩擦力:f=μmgcos30°
设滑块在斜面上通过的总路程为S,则:△Ep=fS
联立三式并代入数据得:S=5.4m
(4)质点第2次由B点沿斜面上滑的距离为L2.则有:mg(L-L2)sin30°-μmgcos37°•(L+L1+L2)=0
解得:L2=($\frac{1}{3}$)2L
同理知:质点第n次由B点沿斜面上滑的距离Ln为:Ln=($\frac{1}{3}$)2L
所以质点从开始到第6次经过B点的过程中,在斜面上通过的路程为:
S=L+2(L1+L2)=5.1m
Q=μmgcos30°S=12.75J
答:
(1)质点第1次经过B点时对圆弧轨道的压力为30N.
(2)质点从A到D的过程中质点下降的高度为0.9m.
(3)在斜面上通过的总路程为5.4m.
(4)质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量为12.75J.
点评 本题考查了考查了动能定理和牛顿第二定律,综合性较强,难度中等,关键是理清运动过程,选择合适的过程运用动能定理进行求解.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | 地球同步卫星和地球同步,因此同步卫星的高度和线速度大小是一定的 | |
| B. | 地球同步卫星的角速度虽被确定,但高度和速度可以选择,高度增加,速度增大,高度降低,速度减小 | |
| C. | 地球同步卫星只能定点在赤道上空,相对地面可以运动 | |
| D. | 以上均不正确 |
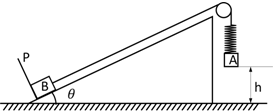 如图所示,固定在水平面上的光滑斜面倾角为30°,物体A、B通过细绳及轻弹簧连接于光滑轻滑轮两侧,P为固定在斜面上且与斜面垂直的光滑挡板,物体A、B的质量分别为m和4m,开始时用手托住物体,滑轮两边的细绳恰好伸直,且左边的细绳与斜面平行,弹簧处于原长状态,A距离地面高度为h时开始下落,在A下落至地面前的瞬间,物体B恰好对挡板无压力.空气阻力不计,下列关于物体A的说法正确的是( )
如图所示,固定在水平面上的光滑斜面倾角为30°,物体A、B通过细绳及轻弹簧连接于光滑轻滑轮两侧,P为固定在斜面上且与斜面垂直的光滑挡板,物体A、B的质量分别为m和4m,开始时用手托住物体,滑轮两边的细绳恰好伸直,且左边的细绳与斜面平行,弹簧处于原长状态,A距离地面高度为h时开始下落,在A下落至地面前的瞬间,物体B恰好对挡板无压力.空气阻力不计,下列关于物体A的说法正确的是( )| A. | 在下落至地面前的过程中机械能守恒 | |
| B. | 在下落至地面前的瞬间速度一定为零 | |
| C. | 在下落至地面前的过程中对轻弹簧做的功为mgh | |
| D. | 在下落至地面前的过程中,可能一直在做加速运动 |
 在如图所示的电路中,电源的负极接地,其电动势为E,内电阻为r,R1,R2为定值电阻,R3为滑动变阻器,C为电容器,A、V分别为理想电流表和理想电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法正确的是( )
在如图所示的电路中,电源的负极接地,其电动势为E,内电阻为r,R1,R2为定值电阻,R3为滑动变阻器,C为电容器,A、V分别为理想电流表和理想电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法正确的是( )| A. | 电压表表示数变小,电流表示数变大 | |
| B. | 电容器C所带电荷量增多 | |
| C. | 电容量内M点的电势降低 | |
| D. | 若将电容器的下极板上移少许,则电荷在M点所具有的电势能减小 |
 如图所示为理想变压器原线圈所接正弦交流电源两端的电压-时间图象.原、副线圈匝数比n1:n2=10:1,串联在原线圈电路中交流电流表的示数为1A,则( )
如图所示为理想变压器原线圈所接正弦交流电源两端的电压-时间图象.原、副线圈匝数比n1:n2=10:1,串联在原线圈电路中交流电流表的示数为1A,则( )| A. | 变压器原线圈所接交流电压的有效值为311V | |
| B. | 变压器输出端所接电压表的示数为22$\sqrt{2}$V | |
| C. | 变压器输出端交变电流的频率为50Hz | |
| D. | 变压器的输出功率为220$\sqrt{2}$W |
 如图所示,水平地面上放着一个画架,它的前支架是固定而后支架可前后移动,画架上静止放着一幅重为G的画.下列说法正确的是( )
如图所示,水平地面上放着一个画架,它的前支架是固定而后支架可前后移动,画架上静止放着一幅重为G的画.下列说法正确的是( )| A. | 画架对画的作用力的大小大于G | |
| B. | 画架对画的作用力的大小等于G | |
| C. | 若后支架向前移动稍许后,画架对画作用力比移动前的小 | |
| D. | 若后支架向前移动稍许后,画架对画作用力的大小保持不变 |
 如图所示,桌面离地高度为h=1m,质量为1kg的小球,从离桌面H=2m高处由静止下落.若以桌面为参考平面,则小球落地时的重力势能及整个过程中小球重力做功分别为(g=10m/s2)( )
如图所示,桌面离地高度为h=1m,质量为1kg的小球,从离桌面H=2m高处由静止下落.若以桌面为参考平面,则小球落地时的重力势能及整个过程中小球重力做功分别为(g=10m/s2)( )| A. | 10J,10J | B. | -10J,30J | C. | -10J,10J | D. | 10J,30J |
 (1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端水平;实验时,每次使小球由静止滚下都应注意从同一高度.
(1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端水平;实验时,每次使小球由静止滚下都应注意从同一高度. 某同学为了测定一根轻弹簧压缩到最短时具有的弹性势能的大小,将弹簧的一端固定在光滑水平桌面上,如图所示,用已知质量为m的钢球将弹簧压缩至最短,而后突然释放,弹簧的弹性势能转化为钢球的动能,钢球将沿水平方向飞出桌面,实验时:
某同学为了测定一根轻弹簧压缩到最短时具有的弹性势能的大小,将弹簧的一端固定在光滑水平桌面上,如图所示,用已知质量为m的钢球将弹簧压缩至最短,而后突然释放,弹簧的弹性势能转化为钢球的动能,钢球将沿水平方向飞出桌面,实验时: