题目内容
【题目】如图所示，在某空间存在一面积足够大的匀强磁场区域，在该区域中心有一半径为R的圆，O为圆心，园内的磁场垂直纸面向里，圆外的磁场垂直纸面向外，磁场的磁感应强度为B。如果在P点有一质量为m、电荷量为q的带正电粒子沿半径方向射入，它在磁场中做圆周运动的轨迹半径也为R，求：
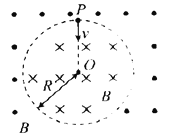
（1）带电粒子的初速度大小；
（2）带电粒子回到P点所需的时间。
【答案】(1) 
(2) 
【解析】试题分析：根据洛伦兹力提供向心力，即可求出带电粒子的初速度大小；画出粒子运动轨迹，结合粒子在磁场中做圆周运动的周期，即可求出带电粒子回到P点所需的时间。
（1）由牛顿第二定律和洛伦兹力公式可得：
解得：
（2）因为粒子在磁场中做圆周运动的轨迹半径也为R，所以它在圆形区域内的轨迹是四分之一圆弧，如图所示，是圆
的一部分；离开圆形区域后，所受洛伦兹力方向相反，以
为圆心做圆周运动，经过四分之三弧长后又进入圆形区域……，这样依次以、、
为圆心做部分圆周运动后又回到P点。
粒子在磁场中做圆周运动的周期为：
，
所以带电粒子回到P点所需的时间为：
练习册系列答案
智能训练练测考系列答案
相关题目
