题目内容
【题目】如图所示,位于竖直平面内的轨道,由一段倾斜的直轨道AB和光滑半圆形轨道BC平滑连接而成 ,AB的倾角为30°,半圆形轨道的半径R=0.1 m ,直径BC竖直.质量m=1 kg的小物块从倾斜轨道上距半圆形轨道底部高为h处由静止开始下滑,经B点滑上半圆形轨道.已知物块与倾斜轨道间的动摩擦因数为![]() ,
,
g取10m/s2,不计小物体在B点处能量的损失.


(1) 若h=1m,求物块运动到圆轨道最低点B时对轨道的压力;
(2) 若物块能到达圆轨道的最高点C,求h的最小值;
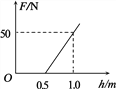
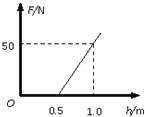
(3) 求物块经最高点C时对轨道压力F随高度h的变化关系,并在图示坐标系中作出F-h图象.
【答案】(1)110N (2)0.5m (3)![]()
【解析】(1)设物块运动圆轨道最低点B时速度大小为v,所受的支持力为N.
根据动能定理有: ![]()
在B点,根据牛顿第二定律有: ![]()
代入数据,解得 N=110N
根据牛顿第三定律知,物块对轨道的压力大小为110N,方向竖直向下.
(2)设物块恰好能到达圆轨道的最高点C,此时对应的高度为hmin,C点的速度为v0.
根据动能定理有: ![]()
经最高点C时,根据向心力公式有: ![]()
代入数据,解得 hmin=0.5m
(3)设物块到达圆轨道最高点时的速度为v,轨道对物块的弹力大小为FN.
根据动能定理有: ![]()
经最高点C,根据向心力公式有: ![]()
解得 FN=100h-50(N)(h≥0.5m)
则压力 F=FN=100h-50(N)(h≥0.5m)
作出F-h图象如图.

练习册系列答案
相关题目