题目内容
20.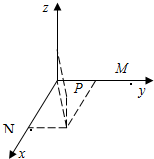 空间有一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点的坐标为$(a,\frac{a}{2},\frac{a}{2})$.已知电场方向平行于直线MN,M点电势为0,N点电势为1V,则P点的电势为( )
空间有一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点的坐标为$(a,\frac{a}{2},\frac{a}{2})$.已知电场方向平行于直线MN,M点电势为0,N点电势为1V,则P点的电势为( )| A. | $\frac{3}{4}$V$\frac{{\sqrt{2}}}{2}$V | B. | $\frac{{\sqrt{3}}}{2}$V | C. | $\frac{1}{4}V$ | D. | $\frac{3}{4}V$ |
分析 将电场强度沿坐标轴方向正交分解,求出轴向的E的分量值,再选用U=Ed,求得电势差,得电势
解答 解:根据题意已知电场方向平行于直线MN,点M的电势为0,点N的电势为1V,故
UNM=E•$\sqrt{2}$a=1V ①
将电场强度沿着+x方向和+y方向正交分解,设合场强为E,则+x和+y方向的分量分别为:
Ex=$\frac{\sqrt{2}}{2}$E,Ey=$\frac{\sqrt{2}}{2}$E ②
设P在x0y平面上的投影为P′点,投影点的坐标为:(a,$\frac{a}{2}$,0)
则 UNP=UNP′=Ey•$\frac{a}{2}$=$\frac{\sqrt{2}}{2}$E$•\frac{a}{2}$=$\frac{1}{4}$V (由①②式得)
又因N点电势为1V,则P′电势为$\frac{3}{4}$V,即P点电势为$\frac{3}{4}$V
则 A B C 错误,D正确
故选:D
点评 本题关键运用正交分解法,将电场沿着坐标轴方向正交分解,然后由U=Ed求解.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
15.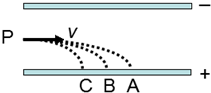 有三个质量相等,分别带正电、负电和不带电的小球,从上、下带电平行金属板间的P点以相同速率垂直电场方向射入电场,分别落在A、B、C三点,如图,则( )
有三个质量相等,分别带正电、负电和不带电的小球,从上、下带电平行金属板间的P点以相同速率垂直电场方向射入电场,分别落在A、B、C三点,如图,则( )
 有三个质量相等,分别带正电、负电和不带电的小球,从上、下带电平行金属板间的P点以相同速率垂直电场方向射入电场,分别落在A、B、C三点,如图,则( )
有三个质量相等,分别带正电、负电和不带电的小球,从上、下带电平行金属板间的P点以相同速率垂直电场方向射入电场,分别落在A、B、C三点,如图,则( )| A. | A球带负电,B球不带电,C球带正电 | |
| B. | 三个小球在电场中的运动时间相等 | |
| C. | 在电场中加速度的关系是aC>aB>aA | |
| D. | 到达正极板时的动能关系是EC<EB<EA |
12.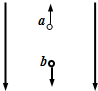 在竖直向下的匀强电场中,有a、b两个带电液滴,分别竖直向上和向下做匀速直线运动,液滴间相互作用力不计,则( )
在竖直向下的匀强电场中,有a、b两个带电液滴,分别竖直向上和向下做匀速直线运动,液滴间相互作用力不计,则( )
 在竖直向下的匀强电场中,有a、b两个带电液滴,分别竖直向上和向下做匀速直线运动,液滴间相互作用力不计,则( )
在竖直向下的匀强电场中,有a、b两个带电液滴,分别竖直向上和向下做匀速直线运动,液滴间相互作用力不计,则( )| A. | a、b一定带同种电荷 | B. | a的电势能和机械能的总和增大 | ||
| C. | a的电势能减小 | D. | b的重力势能增大 |
9.发射“嫦娥三号”卫星的大致过程是:先将卫星送入绕地球椭圆轨道,再点火加速运动至月球附近被月球“俘获”而进入较大的绕月椭圆轨道,又经三次点火制动“刹车”后进入近月圆轨道,在近月圆轨道上绕月运行的周期是T=127分钟.又知月球表面的重力加速度为g′=$\frac{g}{6}$(g是地球表面的重力加速度g=10m/s2).下列说法中正确的是( )
| A. | 仅凭上述信息及T、g′能算出月球的半径 | |
| B. | 仅凭上述信息及T、g′能算出月球上的第一宇宙速度 | |
| C. | 仅凭上述信息及T、g′能算出月球的质量和密度 | |
| D. | 卫星沿绕地球椭圆轨道运行时,卫星上的仪器处于失重状态 |
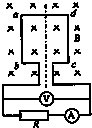 如图所示,线圈abcd的面积S=0.05m2,共N=100匝;线圈电阻为r=1Ω,外接电阻R=9Ω,匀强磁场的磁感强度为B=0.2T,线圈以ω=20rad/s匀速转动,电路中电流表和电压表为理想电表,现从线圈处于中性面开始计时,求:
如图所示,线圈abcd的面积S=0.05m2,共N=100匝;线圈电阻为r=1Ω,外接电阻R=9Ω,匀强磁场的磁感强度为B=0.2T,线圈以ω=20rad/s匀速转动,电路中电流表和电压表为理想电表,现从线圈处于中性面开始计时,求: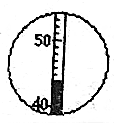 实验室用温度计是利用液体热胀冷缩的性质制成的,在使用温度计时,要将温度计与被测物体充分接触,并保持足够长时间,在读取数据时,温度计不能(填“能”或“不能”)从测量对象移开,读数时视线应与温度计的标尺垂直,如图所示,其示数为44.0℃.
实验室用温度计是利用液体热胀冷缩的性质制成的,在使用温度计时,要将温度计与被测物体充分接触,并保持足够长时间,在读取数据时,温度计不能(填“能”或“不能”)从测量对象移开,读数时视线应与温度计的标尺垂直,如图所示,其示数为44.0℃.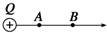 如图所示,在点电荷+Q激发的电场中有A、B两点,将质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)分别从A点由静止释放到达B点时,它们的速度大小之比为$\sqrt{2}$:1,动能之比为1:2.
如图所示,在点电荷+Q激发的电场中有A、B两点,将质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)分别从A点由静止释放到达B点时,它们的速度大小之比为$\sqrt{2}$:1,动能之比为1:2.