题目内容
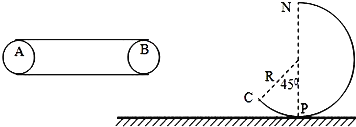
【题目】如图所示,A、B是水平传送带的两个端点,起初以![]() 的速度顺时针运转.今将一小物块(可视为质点)无初速度地轻放在A处,同时传送带以
的速度顺时针运转.今将一小物块(可视为质点)无初速度地轻放在A处,同时传送带以![]() 的加速度加速运转,物体和传送带间的动摩擦因素为0.2,水平桌面右侧有一竖直放置的光滑轨道CPN,其形状为半径R=0.8m的圆环剪去了左上角
的加速度加速运转,物体和传送带间的动摩擦因素为0.2,水平桌面右侧有一竖直放置的光滑轨道CPN,其形状为半径R=0.8m的圆环剪去了左上角![]() 的圆弧,PN为其竖直直径,C点与B点的竖直距离为h=0.8m,物体离开传送带后由C点恰好无碰撞落入轨道.取
的圆弧,PN为其竖直直径,C点与B点的竖直距离为h=0.8m,物体离开传送带后由C点恰好无碰撞落入轨道.取![]() ,求:
,求:
(1)物块离开B端瞬间的速度![]() 的大小
的大小
(2)AB间的水平距离L
(3)判断物体能否沿圆轨道到达N点.
【答案】(1)![]() ,(2)7m,(3)物块不能到达N点.
,(2)7m,(3)物块不能到达N点.
【解析】(1)小物块从B到C,由平抛运动规律和在C点的角度关系,联立求B点的速度;(2)假设小物块在传送带上先做匀加速后做匀速运动,求出小物块与传送带共速的速度,再与物块到达B的速度进行比较,然后再算出共速的时间,求出AB间的水平距离L;(3)从B到N由能量守恒定律求出小物块在N点的速度,在N点由牛顿第二定律求出在N点轨道的支持力,再与通过N点的临界条件进行分析判断.
(1)小物块平抛运动,由平抛运动规律得: ![]() 、
、![]()
在C点由几何关系得: ![]()
联立解得: ![]() ,
, ![]()
(2)小物块刚放上传送带时,与传送带相对滑动,假设经![]() 秒与皮带共速,再经
秒与皮带共速,再经![]() 秒到达B点
秒到达B点
在加速阶段,由牛顿第二定律: ![]()
由运动学公式得:对物块有![]() ,对传送带有
,对传送带有![]()
联立解得: ![]()
![]() ,说明假设合理
,说明假设合理
由![]() 解得:
解得: ![]()
所以AB间的水平距离 ![]()
(3)设小物块能沿轨道通过N点,到达N点的速度为![]() ,到N点瞬间受到轨道的压力为F
,到N点瞬间受到轨道的压力为F
则物块由B到N,由能量守恒定律得: ![]()
解得: ![]()
在N点时: ![]()
解得: ![]()
显然假设不合理,即物块不能到达N

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目