题目内容
如图2－28，有一水平传送带以2m／s的速度匀速运动，现将一物体轻轻放在传送带上，若物体与传送带间的动摩擦因数为0.5，则传送带将该物体传送10m的距离所需时间为多少？
传送10m所需时间为t=0.4＋4.8=5.2s
【错解】由于物体轻放在传送带上，所以v0=0，物体在竖直方向合外力为零，在水平方向受到滑动摩擦力（传送带施加），做v0=0的匀加速运动，位移为10m。
据牛顿第二定律F=ma有f=μmg=ma，a=μg=5m/s2
【错解原因】上述解法的错误出在对这一物理过程的认识。传送带上轻放的物体的运动有可能分为两个过程。一是在滑动摩擦力作用下作匀加速直线运动；二是达到与传送带相同速度后，无相对运动，也无摩擦力，物体开始作匀速直线运动。关键问题应分析出什么时候达到传送带的速度，才好对问题进行解答。
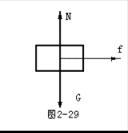
【分析解答】以传送带上轻放物体为研究对象，如图2－29在竖直方向受重力和支持力，在水平方向受滑动摩擦力，做v0=0的匀加速运动。
据牛二定律F=ma
有水平方向：f="ma " ①
竖直方向：N-mg="0 " ②
f="μN " ③
由式①，②，③解得a=5m／s2
设经时间tl，物体速度达到传送带的速度，据匀加速直线运动的速度公式
v0=v0+at ④
解得t1=0.4s
物体位移为0.4m时，物体的速度与传送带的速度相同，物体0.4s后无摩擦力，开始做匀速运动
S2=v2t2 ⑤
因为S2=S-S1=10—0.4=9.6（m），v2=2m／s
代入式⑤得t2=4.8s
则传送10m所需时间为t=0.4＋4.8=5.2s。
练习册系列答案
相关题目
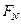）的作用下，一辆质量为M、倾角为
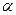的斜面小车从静止开始沿水平地面运动；车上有一个质量为m的滑块，其受力及相应的合力（∑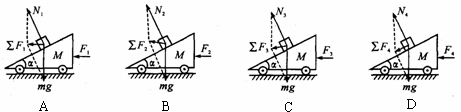
圆弧CD相切；ED为地面.已知儿童在滑槽上滑动时的动摩擦因数是0.5，在B点由斜面转到水平面的运动速率不变，A点离地面的竖直高度AE为2 m.取g="10" m/s2,试求：
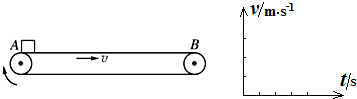无初速度地放在左侧传动轮正上方的传送带A点后，经过一段时间运动到右侧传动轮正上方的B点．行李与传送带之间的动摩擦因数μ=0.2，A、B间的距离L=2m，取g=10m/s2．
