题目内容
10. 如图所示,绕过光滑钉子O的细绳,两端分别拴有A、B两个小球,A球的质量是B球的2倍.现将两球从距地面高度为h处由静止释放.若细绳足够长,细绳的质量、空气的阻力均不计.则B球上升到距地面的最大高度为( )
如图所示,绕过光滑钉子O的细绳,两端分别拴有A、B两个小球,A球的质量是B球的2倍.现将两球从距地面高度为h处由静止释放.若细绳足够长,细绳的质量、空气的阻力均不计.则B球上升到距地面的最大高度为( )| A. | h | B. | $\frac{7}{3}h$ | C. | $\frac{8}{3}h$ | D. | $\frac{10}{3}h$ |
分析 由机械能守恒可判定B的最大上升高度,从而得到离地最大高度.
解答 解:
对系统由机械能守恒可得:
2mgh-mgh=$\frac{1}{2}×3m×{v}^{2}$,
对B在A落地之后:
$\frac{1}{2}m{v}^{2}=mgh′$,
解得:
$h′=\frac{1}{3}h$,
故B的离地最大高度为:
$H=h′+2h=\frac{7}{3}h$,
故B正确,ACD错误.
故选:B.
点评 该题的关键是用好系统的机械能守恒,单独对A或对B机械能都不守恒,这就是对系统机械能守恒的巧妙利用.

练习册系列答案
相关题目
20.根据学过的物理知识判断,下列说法中正确的是( )
| A. | 小轿车车尾的导电链是为了防止静电积聚 | |
| B. | 洗衣机的脱水筒是利用离心运动把附着在衣服上的水分甩掉 | |
| C. | 乘坐汽车时要系好安全带,这是为了防止汽车突然加速而对乘客造成伤害 | |
| D. | 夜间高压线周围有时会出现一层绿色光晕,俗称电晕,这是一种微弱的尖端放电 |
5. 在一粗细均匀且两端封闭的U形玻璃管内,有一段水银柱将A和B两端的气体隔开,如图所示,在室温下,A、B两端气体的体积都是V,管内水银面的高度差为△h,现将它竖直地全部浸没在沸水中,则( )
在一粗细均匀且两端封闭的U形玻璃管内,有一段水银柱将A和B两端的气体隔开,如图所示,在室温下,A、B两端气体的体积都是V,管内水银面的高度差为△h,现将它竖直地全部浸没在沸水中,则( )
 在一粗细均匀且两端封闭的U形玻璃管内,有一段水银柱将A和B两端的气体隔开,如图所示,在室温下,A、B两端气体的体积都是V,管内水银面的高度差为△h,现将它竖直地全部浸没在沸水中,则( )
在一粗细均匀且两端封闭的U形玻璃管内,有一段水银柱将A和B两端的气体隔开,如图所示,在室温下,A、B两端气体的体积都是V,管内水银面的高度差为△h,现将它竖直地全部浸没在沸水中,则( )| A. | A端气体体积比B端大 | B. | △h增大 | ||
| C. | A端气体压强比B端大 | D. | △h不变 |
15.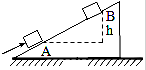 如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )
如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )
 如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )
如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )| A. | 物体所受重力做的功为mgh | |
| B. | 恒力F与摩擦力的合力做功为mgh | |
| C. | 物体所受的支持力与摩擦力的合力做功为mgh | |
| D. | 物体所受各力的合力做功为mgh |
19.一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是( )
| A. | 增大入射光的频率,金属的逸出功将增大 | |
| B. | 增大入射光的频率,光电子的最大初动能将增大 | |
| C. | 增大入射光的强度,光电子的最大初动能将增大 | |
| D. | 延长入射光照射时间,光电子的最大初动能将增大 |
20.如图甲所示,理想变压器原、副线圈的匝数之比为44:5,b是原线圈的中心抽头,S为单刀双掷开关,负载电阻R=25Ω,电表均为理想电表.在原线圈c、d两端接入如图乙所示的正弦交流电,下列说法中正确的是( )
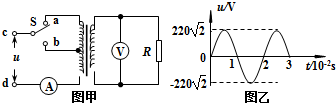

| A. | 当S与a连接时,电流表的示数为1A | |
| B. | 当S与b连接时,电压表的示数为50$\sqrt{2}$V | |
| C. | 将S由a拨到b,电阻R消耗的功率增大为原来的4倍 | |
| D. | 无论S接a还是接b,1s内电阻R上电流方向都改变50次 |
 如图所示,线圈的横截面积为S,共有N匝,总电阻为R,垂直于线圈截面的磁场在均匀变化(方向如图所示).线圈与水平放置相距为d的两平行金属板M,N相连,M、N间有磁感应强度为B的匀强磁场.一电子以速度v射入两极间,要使电子能匀速向右运动,求线圈内磁场的变化率.
如图所示,线圈的横截面积为S,共有N匝,总电阻为R,垂直于线圈截面的磁场在均匀变化(方向如图所示).线圈与水平放置相距为d的两平行金属板M,N相连,M、N间有磁感应强度为B的匀强磁场.一电子以速度v射入两极间,要使电子能匀速向右运动,求线圈内磁场的变化率.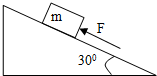 如图所示,倾角为30°的斜面上放一质量为10㎏的木块,木块与斜面之间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,用一平行于斜面的力F向上推木块,欲使木块静止在斜面上,求推力F的范围?(假设最大静摩擦力等于滑动摩擦力,g=10m/s2)
如图所示,倾角为30°的斜面上放一质量为10㎏的木块,木块与斜面之间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,用一平行于斜面的力F向上推木块,欲使木块静止在斜面上,求推力F的范围?(假设最大静摩擦力等于滑动摩擦力,g=10m/s2) 如图所示,一块物块m静止在斜面上,斜面匀速地竖直向上移动距离h,则摩擦力、弹力、重力对物块做的功分别为多少?
如图所示,一块物块m静止在斜面上,斜面匀速地竖直向上移动距离h,则摩擦力、弹力、重力对物块做的功分别为多少?