题目内容
18.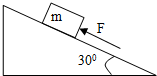 如图所示,倾角为30°的斜面上放一质量为10㎏的木块,木块与斜面之间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,用一平行于斜面的力F向上推木块,欲使木块静止在斜面上,求推力F的范围?(假设最大静摩擦力等于滑动摩擦力,g=10m/s2)
如图所示,倾角为30°的斜面上放一质量为10㎏的木块,木块与斜面之间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,用一平行于斜面的力F向上推木块,欲使木块静止在斜面上,求推力F的范围?(假设最大静摩擦力等于滑动摩擦力,g=10m/s2)
分析 对物块受力分析,当推力F最大时,物块的最大静摩擦力沿斜面向下,当推力F最小时,物块的最大静摩擦力沿斜面向上,根据平衡求出推力F的最大值和最小值,从而得出范围.
解答 解:当F最大时,最大静摩擦力方向沿斜面向下,有:F1=mgsin30°+μmgcos30°=100×$\frac{1}{2}$+$\frac{\sqrt{3}}{6}×100×\frac{\sqrt{3}}{2}$N=75N.
当F最小时,最大静摩擦力沿斜面向上,有:F2+μmcos30°=mgsin30°,
解得F2=mgsin30°-μmgcos30°=$100×\frac{1}{2}-\frac{\sqrt{3}}{6}×100×\frac{\sqrt{3}}{2}$N=25N.
则推力F的范围为:25N≤F≤75N.
答:推力F的范围为25N≤F≤75N.
点评 解决本题的关键抓住临界状态,结合共点力平衡求出推力的最大值和最小值,难度不大.

练习册系列答案
相关题目
9.用伏安法测金属丝的电阻Rx.实验所用器材为:电池组(电动势为3V,内阻约1Ω)、电流表(内阻约0.1Ω)、电压表(内阻约3kΩ)、滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干.
(1)某小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
由以上数据可知,他们测量Rx是采用图1中的甲图(选填“甲”或“乙”)

(2)图2是测量Rx的实验器材实物图,图中已连接了部分导线,滑动变阻器的滑片P置于变阻器的一端.请根据图1所选的电路图,补充完成图2中实物间的连线,并使闭合开关的瞬间,电压表或电流表不至于被烧坏.
(3)这个小组的同学在坐标纸上建立U、I坐标系,如图3所示,请根据实验测量数据,在图3中标出7次测量数据坐标点,并描绘出U-I图线.由图线得到金属丝的阻值Rx=4.5Ω(保留两位有效数字).
(1)某小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.10 | 0.30 | 0.70 | 1.00 | 1.50 | 1.70 | 2.30 |
| I/A | 0.020 | 0.060 | 0.160 | 0.220 | 0.340 | 0.460 | 0.520 |

(2)图2是测量Rx的实验器材实物图,图中已连接了部分导线,滑动变阻器的滑片P置于变阻器的一端.请根据图1所选的电路图,补充完成图2中实物间的连线,并使闭合开关的瞬间,电压表或电流表不至于被烧坏.
(3)这个小组的同学在坐标纸上建立U、I坐标系,如图3所示,请根据实验测量数据,在图3中标出7次测量数据坐标点,并描绘出U-I图线.由图线得到金属丝的阻值Rx=4.5Ω(保留两位有效数字).
3.一束白光垂直于三棱镜的一个面入射发生色散( )
| A. | 棱镜对各色光的折射率不同 | |
| B. | 红光比蓝光通过棱镜所用的时间短 | |
| C. | 黄光比绿光偏转的角度小 | |
| D. | 在棱镜中,速度较大的单色光偏转的角度也较大 |
10. 如图所示,绕过光滑钉子O的细绳,两端分别拴有A、B两个小球,A球的质量是B球的2倍.现将两球从距地面高度为h处由静止释放.若细绳足够长,细绳的质量、空气的阻力均不计.则B球上升到距地面的最大高度为( )
如图所示,绕过光滑钉子O的细绳,两端分别拴有A、B两个小球,A球的质量是B球的2倍.现将两球从距地面高度为h处由静止释放.若细绳足够长,细绳的质量、空气的阻力均不计.则B球上升到距地面的最大高度为( )
 如图所示,绕过光滑钉子O的细绳,两端分别拴有A、B两个小球,A球的质量是B球的2倍.现将两球从距地面高度为h处由静止释放.若细绳足够长,细绳的质量、空气的阻力均不计.则B球上升到距地面的最大高度为( )
如图所示,绕过光滑钉子O的细绳,两端分别拴有A、B两个小球,A球的质量是B球的2倍.现将两球从距地面高度为h处由静止释放.若细绳足够长,细绳的质量、空气的阻力均不计.则B球上升到距地面的最大高度为( )| A. | h | B. | $\frac{7}{3}h$ | C. | $\frac{8}{3}h$ | D. | $\frac{10}{3}h$ |
8.已知氘核的平均结合能是1.09MeV,氚核的平均结合能是2.78MeV,氦核的平均结合能是7.03MeV.在某次核反应中,1个氘核和1个氚核结合生成1个氦核并放出17.6MeV的能量,下列说法正确的是( )
| A. | 这是一个裂变反应 | |
| B. | 核反应方程式为${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| C. | 目前核电站都采用上述核反应发电 | |
| D. | 该核反应会有质量亏损 |
 如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与平板小车右端平滑对接.小车质量M=3kg,车长L=2.06m.现有一质量m=1kg的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:
如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与平板小车右端平滑对接.小车质量M=3kg,车长L=2.06m.现有一质量m=1kg的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求: 水平面上静止放置一质量为m=0.2kg的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2秒末到达额定功率,其v-t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,g=10m/s2,电动机与物块间的距离足够远,求:
水平面上静止放置一质量为m=0.2kg的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2秒末到达额定功率,其v-t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,g=10m/s2,电动机与物块间的距离足够远,求: 如图所示,竖直平面内有足够长的光滑的两条竖直平行金属导轨,上端接有一个定值电阻R0,两导轨间的距离L=2m,在虚线的区域内有与导轨平面垂直的匀强磁场,磁感应强度B=0.2T,虚线间的高度h=1m.完全相同的金属棒ab、cd与导轨垂直放置,质量均为m=0.1kg,两棒间用l=2m长的绝缘轻杆连接.棒与导轨间接触良好,两棒电阻皆为r=0.3Ω,导轨电阻不计,已知R0=2r.现用一竖直方向的外力从图示位置作用在ab棒上,使两棒以v=5m/s的速度向下匀速穿过磁场区域(不计空气和摩擦阻力,重力加速度g取10m/s2).求:
如图所示,竖直平面内有足够长的光滑的两条竖直平行金属导轨,上端接有一个定值电阻R0,两导轨间的距离L=2m,在虚线的区域内有与导轨平面垂直的匀强磁场,磁感应强度B=0.2T,虚线间的高度h=1m.完全相同的金属棒ab、cd与导轨垂直放置,质量均为m=0.1kg,两棒间用l=2m长的绝缘轻杆连接.棒与导轨间接触良好,两棒电阻皆为r=0.3Ω,导轨电阻不计,已知R0=2r.现用一竖直方向的外力从图示位置作用在ab棒上,使两棒以v=5m/s的速度向下匀速穿过磁场区域(不计空气和摩擦阻力,重力加速度g取10m/s2).求: 如图所示,一质量为m的小车静止在光滑的水平面上,在它的横梁上用长为1m的细线悬挂着质量也为m的小球,开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.试求:(取g=10m/s2)
如图所示,一质量为m的小车静止在光滑的水平面上,在它的横梁上用长为1m的细线悬挂着质量也为m的小球,开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.试求:(取g=10m/s2)