题目内容
10. 如图所示,固定在水平面上的圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧拴接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B一起运动但与B不粘连.求:
如图所示,固定在水平面上的圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧拴接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B一起运动但与B不粘连.求:(1)弹簧的最大弹性势能;
(2)A和B第一次刚要分离时,A、B速度是多大?
(3)A与B第一次分离后,物块A沿圆弧面上升的最大高度.
分析 (1)根据动能定理求出A滑动最低点的速度,对AB组成的系统运用动量守恒,求出A、B碰撞后的速度,再结合能量守恒求出弹簧的最大弹性势能.
(2)A和B第一次刚要分离时速度的大小等于A、B碰撞后的速度大小.
(3)结合能量守恒求出物块A沿圆弧面上升的最大高度.
解答 解:(1)A滑到最低点时速度为v,由动能定理得,
$3mgh=\frac{1}{2}3m{v}^{2}$,
A、B碰撞过程动量守恒,碰后速度为v1,规定向右为正方向,根据动量守恒有:3mv=4mv1,
A、B压缩弹簧至最短,速度为0,最大弹性势能为Ep,对系统由能量守恒得,${E}_{p}=\frac{1}{2}×4m{{v}_{1}}^{2}$,
解得:${E}_{p}=\frac{9}{4}mgh$.
(2)弹簧恢复原长时A、B刚要分开,且二者速度相等都为v1,
由$3mgh=\frac{1}{2}3m{v}^{2}$,3mv=4mv1得,${v}_{1}=\frac{3}{4}\sqrt{2gh}$.
(3)A上升最大高度为h1,速度为0,
根据能量守恒得,$3mg{h}_{1}=\frac{1}{2}×3m{{v}_{1}}^{2}$,
解得${h}_{1}=\frac{9}{16}h$.
答:(1)弹簧的最大弹性势能为$\frac{9}{4}mgh$;
(2)A和B第一次刚要分离时,A、B速度是$\frac{3}{4}\sqrt{2gh}$;
(3)A与B第一次分离后,物块A沿圆弧面上升的最大高度为$\frac{9}{16}h$.
点评 本题关键是明确动量守恒定律和机械能守恒定律成立的条件,明确那个过程动量守恒,那个过程机械能守恒,根据守恒定律列式后联立求解即可.

练习册系列答案
相关题目
4. 如图所示,可看作质点的小物体位于半径为R的半球顶端,若给小物体以水平速度v0时,小物体对球顶恰好无压力,则( )
如图所示,可看作质点的小物体位于半径为R的半球顶端,若给小物体以水平速度v0时,小物体对球顶恰好无压力,则( )
 如图所示,可看作质点的小物体位于半径为R的半球顶端,若给小物体以水平速度v0时,小物体对球顶恰好无压力,则( )
如图所示,可看作质点的小物体位于半径为R的半球顶端,若给小物体以水平速度v0时,小物体对球顶恰好无压力,则( )| A. | 物体将沿着球面做圆周运动 | B. | 物体落地时速度与水平方向成45° | ||
| C. | 物体落地时水平位移为2R | D. | 物体落地时速度大小为$\sqrt{3}$v0 |
1.图(1)为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=6.0m处的质点.图(2)为质点Q的振动图象,下列说法正确的是( )
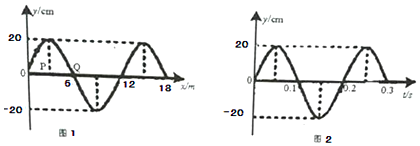

| A. | 这列简谐横波的波速为60m/s | |
| B. | 在t=0.10s时,质点P的运动方向与y轴正方向相同 | |
| C. | 在t=0.10s时,质点Q向y轴负方向运动 | |
| D. | 从t=0.10s到t=0.20s,质点Q通过的路程为20cm | |
| E. | 质点Q简谐运动的表达式为y=0.20sin$\frac{20π}{3}$t(cm) |
5. 一个内壁光滑的圆锥形的轴线垂直水平面,圆锥筒固定,有质量不同的小球A和B沿着筒的内壁在水平面内各自做匀速圆周运动,如图所示,A的运动半径较大,则( )
一个内壁光滑的圆锥形的轴线垂直水平面,圆锥筒固定,有质量不同的小球A和B沿着筒的内壁在水平面内各自做匀速圆周运动,如图所示,A的运动半径较大,则( )
 一个内壁光滑的圆锥形的轴线垂直水平面,圆锥筒固定,有质量不同的小球A和B沿着筒的内壁在水平面内各自做匀速圆周运动,如图所示,A的运动半径较大,则( )
一个内壁光滑的圆锥形的轴线垂直水平面,圆锥筒固定,有质量不同的小球A和B沿着筒的内壁在水平面内各自做匀速圆周运动,如图所示,A的运动半径较大,则( )| A. | A球的角速度必小于B球的角速度 | |
| B. | A球的角速度必等于B球的角速度 | |
| C. | A球的运动周期必大于B球的运动周期 | |
| D. | A球的向心力必等于B球的向心力 |
15.关于摩擦力做功问题,下列叙述中正确的是( )
| A. | 摩擦力总是阻力,故只能做负功 | |
| B. | 静摩擦力出现的地方物体间无相对位移,故肯定不做功 | |
| C. | 摩擦力可能做正功也可能做负功 | |
| D. | 滑动摩擦力对两个相互作用的物体大小相等,方向相反,故对两个物体所做的功大小相同,正负相反 |
2. 如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
 如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )| A. | vA′=-2 m/s,vB′=6 m/s | B. | vA′=2 m/s,vB′=2 m/s | ||
| C. | vA′=1 m/s,vB′=3 m/s | D. | vA′=-3 m/s,vB′=7 m/s |
19.一质量为2kg的物体在5个共点力作用下做匀速直线运动.现撤去其中一个大小为10N的力,其余的力大小和方向均保持不变.下列关于此后该物体运动的说法中,正确的是( )
| A. | 可能做匀减速直线运动,加速度大小为5 m/s2 | |
| B. | 可能做匀速圆周运动,向心加速度大小为5 m/s2 | |
| C. | 可能做匀变速曲线运动,加速度大小为5 m/s2 | |
| D. | 一定做匀变速直线运动,加速度大小为5 m/s2 |
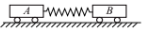 如图所示,两小车A、B置于光滑水平面上,质量分别为m和2m,一轻弹簧两端分别固定在两小车上,开始时弹簧处于拉伸状态,用手固定两小车.现在先释放小车B,当小车B的速度大小为3v时,再释放小车A,此时弹簧仍处于拉伸状态;当小车A的速度大小为v时,弹簧刚好恢复原长.自始至终弹簧都未超出弹性限度.求:
如图所示,两小车A、B置于光滑水平面上,质量分别为m和2m,一轻弹簧两端分别固定在两小车上,开始时弹簧处于拉伸状态,用手固定两小车.现在先释放小车B,当小车B的速度大小为3v时,再释放小车A,此时弹簧仍处于拉伸状态;当小车A的速度大小为v时,弹簧刚好恢复原长.自始至终弹簧都未超出弹性限度.求: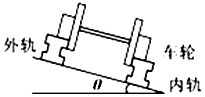 铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则火车不挤压内外轨道,若速度大于$\sqrt{gRtanθ}$则火车挤压外轨道,若速度小于$\sqrt{gRtanθ}$则火车挤压内轨道.(填“内”或“外”)
铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则火车不挤压内外轨道,若速度大于$\sqrt{gRtanθ}$则火车挤压外轨道,若速度小于$\sqrt{gRtanθ}$则火车挤压内轨道.(填“内”或“外”)