题目内容
(13分)如图所示,用完全相同的、劲度系数均为k的轻弹簧A、B、C将两个质量均为m的小球连接并悬挂起来,两小球均处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,已知重力加速度为g,试求出轻弹簧A、B、C各自的伸长量。(所有弹簧形变均在弹性范围内)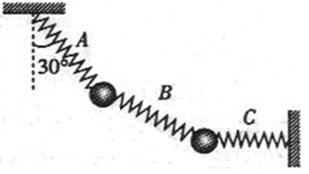
xA= ,xB=
,xB= ,xC=
,xC=
解析试题分析:将两小球看作一个整体,对整体受力分析,可知整体受到重力2mg、弹簧A和C的拉力FA、FC的作用,受力如下图甲所示,根据共点力平衡条件有:FA=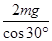 ,FC=2mgtan30°
,FC=2mgtan30°
根据胡克定律有:FA=kxA,FC=kxC
联立以上各式解得弹簧A、C的伸长量分别为:xA= ,xC=
,xC=
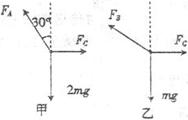
对B、C间的小球进行受力分析,其受力如图乙所示,根据平衡条件有:FB=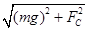 =
=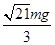
根据胡克定律有:FB=kxB,解得弹簧B的伸长量为:xB=
考点:本题主要考查了共点力平衡条件、胡克定律的应用以及整体法与隔离法的灵活运用问题,属于中档题。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
下面关于惯性的说法中,正确的是
| A.运动速度大的物体比速度小的物体难停下来,所以运动速度大的物体具有较大的惯性 |
| B.物体受的力越大,要它停下来就越困难,所以物体受的力越大,则惯性越大 |
| C.在月球上举重比在地球上容易,所以同一物体在地球上惯性比在月球上大 |
| D.物体含的物质越多,惯性越大 |

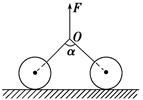
 ,两球与水平地面间的动摩擦因数都为
,两球与水平地面间的动摩擦因数都为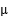 ,且假设最大静摩擦力等于滑动摩擦力,一根轻绳两端固结在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为
,且假设最大静摩擦力等于滑动摩擦力,一根轻绳两端固结在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为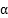 .问当F至少为多大时,两球将会发生滑动?
.问当F至少为多大时,两球将会发生滑动?