题目内容
【题目】物理中存在“通量”这个物理量,“通量”的定义要用到高等数学知识.在高中阶段,对“通量”的定义采用的是简单化处理方法并辅以形象化物理模型进行理解.
(1)“磁通量”就是一种常见的“通量”.在高中阶段我们是这样来定义“磁通量”的:设在磁感应强度为![]() 的匀强磁场中,有一个与磁场方向垂直的平面,面积为
的匀强磁场中,有一个与磁场方向垂直的平面,面积为![]() ,我们把
,我们把![]() 与
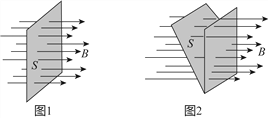
与![]() 的乘积叫做穿过这个面积的磁通量(图1),简称磁通.用字母
的乘积叫做穿过这个面积的磁通量(图1),简称磁通.用字母![]() 表示,则
表示,则![]() .磁通量可以形象地理解为穿过某一面积的磁感线条数的多少.如图2所示,空间存在水平向右的匀强磁场,磁感应强度大小为
.磁通量可以形象地理解为穿过某一面积的磁感线条数的多少.如图2所示,空间存在水平向右的匀强磁场,磁感应强度大小为![]() .一个面积为
.一个面积为![]() 的矩形线圈与竖直面间的夹角为
的矩形线圈与竖直面间的夹角为![]() ,试求穿过该矩形线圈的磁通量
,试求穿过该矩形线圈的磁通量![]() .
.
(2)“电通量”也是一种常见的“通量”.在定义“电通量”时只需要把“磁通量”中的磁感应强度![]() 替换为电场强度
替换为电场强度![]() 即可.请同学们充分运用类比的方法解决以下问题.已知静电力常量为
即可.请同学们充分运用类比的方法解决以下问题.已知静电力常量为![]() .
.
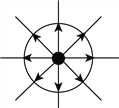

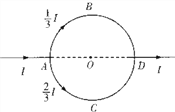
图3 图4
a.如图3所示,空间存在正点电荷![]() ,以点电荷为球心作半径为
,以点电荷为球心作半径为![]() 的球面,试求通过该球面的电通量
的球面,试求通过该球面的电通量![]() .
.
b.上述情况映射的是静电场中“高斯定理”,“高斯定理”可以从库仑定律出发得到严格证明.“高斯定理”可表述为:通过静电场中任一闭合曲面的电通量等于闭合曲面内所含电荷量![]() 与
与![]() 的乘积,即
的乘积,即![]() ,其中
,其中![]() 为静电力常量.试根据“高斯定理”证明:一个半径为
为静电力常量.试根据“高斯定理”证明:一个半径为![]() 的均匀带电球体(或球壳)在外部产生的电场,与一个位于球心的、电荷量相等的点电荷产生的电场相同,球外各点的电场强度也是
的均匀带电球体(或球壳)在外部产生的电场,与一个位于球心的、电荷量相等的点电荷产生的电场相同,球外各点的电场强度也是![]() ,式中
,式中![]() 是球心到该点的距离,
是球心到该点的距离, ![]() 为整个球体所带的电荷量.
为整个球体所带的电荷量.
【答案】(1)![]() (2)a.
(2)a. ![]() b.
b. ![]()
【解析】(1)![]() .
.
(2)a.根据点电荷的场强公式,求得球面上各处的电场强度大小为![]() ,
,
由于球面上各处电场强度方向都与球面垂直,故通过球面的电通量为,
![]() ,
,
b.证明:过距离球心距离![]() 的点作一球面,根据对称性可知该球面上各点场强大小相等,方向处处球面垂直.设该点的电场强度为
的点作一球面,根据对称性可知该球面上各点场强大小相等,方向处处球面垂直.设该点的电场强度为![]() ,通过该球面的电通量为
,通过该球面的电通量为![]() ,则
,则
![]() ,
,
由高斯定理知, ![]() ,
,
所以有![]() ,
,
化简得![]() ,这就是球心处的点电荷
,这就是球心处的点电荷![]() 在
在![]() 处产生的场强,证明完毕.
处产生的场强,证明完毕.