题目内容
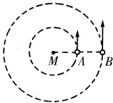
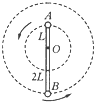
如图所示,轻质杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,当球B运动到最低点时,杆对球B的作用力大小为2mg,已知当地重力加速度为g,求此时:
(1)球B转动的角速度大小;
(2)A球对杆的作用力大小以及方向;
(3)在点O处,轻质杆对水平转动轴的作用力大小和方向.
(1)球B转动的角速度大小;
(2)A球对杆的作用力大小以及方向;
(3)在点O处,轻质杆对水平转动轴的作用力大小和方向.

(1)小球B受重力和弹力的合力提供向心力,根据牛顿第二定律:
F1-mg=mω2(2L)
其中:
F1=2mg
联立解得:
ω=
(2)A球的角速度等于B球的角速度,为
;
设杆对A球是向下的拉力,根据牛顿第二定律,有:
F2+mg=mω2L
解得:
F2=-
mg<0,故假设不成立,是向上的支持力;
(3)根据牛顿第三定律,球A对杆有向下的压力,为:F2′=
mg;
球B对杆有向下的拉力,为:F1′=2mg;
杆受力平衡,故轴对杆的弹力向上,为:
N=F1′+F2′=2.5mg;
根据牛顿第三定律,杆对转轴的作用力向下,为2.5mg;
答:(1)球B转动的角速度大小为
;
(2)A球对杆的作用力大小为
mg,方向为竖直向上;
(3)在点O处,轻质杆对水平转动轴的作用力大小为2.5mg,方向为竖直向下.
F1-mg=mω2(2L)
其中:
F1=2mg
联立解得:
ω=
|
(2)A球的角速度等于B球的角速度,为
|
设杆对A球是向下的拉力,根据牛顿第二定律,有:
F2+mg=mω2L
解得:
F2=-
| 1 |
| 2 |
(3)根据牛顿第三定律,球A对杆有向下的压力,为:F2′=
| 1 |
| 2 |
球B对杆有向下的拉力,为:F1′=2mg;
杆受力平衡,故轴对杆的弹力向上,为:
N=F1′+F2′=2.5mg;
根据牛顿第三定律,杆对转轴的作用力向下,为2.5mg;
答:(1)球B转动的角速度大小为
|
(2)A球对杆的作用力大小为
| 1 |
| 2 |
(3)在点O处,轻质杆对水平转动轴的作用力大小为2.5mg,方向为竖直向下.

练习册系列答案
相关题目