题目内容
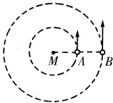
如图所示,有A、B两颗行星绕同一颗恒星M做圆周运动,旋转方向相同,A行星的周期为T1,B行星的周期为T2,在某一时刻两行星相距最近,则( )
| A.经过时间t=T1+T2,两行星再次相距最近 | ||
B.经过时间t=
| ||
C.经过时间t=
| ||
D.经过时间t=
|

A、B、根据万有引力提供向心力,列出等式:
=mω2r
解得:ω=
所以ωA>ωB
A行星的周期为T1,B行星的周期为T2,
所以T1=
,T2=
两行星相距最近时,两行星应该在同一半径方向上.
所以当A比B多转一圈时两行星再次相距最近,列出等式:
(
-
)t=2π
t=
,故A错误,故B正确.
C、D、两行星相距最远时,两行星应该在同一直径上.
所以当A比B多转半圈时两行星相距最远,列出等式:
(
-
)t′=π
t′=
,故C错误,D正确.
故选:BD.
| GMm |
| r2 |
解得:ω=
|
所以ωA>ωB
A行星的周期为T1,B行星的周期为T2,
所以T1=
| 2π |
| ωA |
| 2π |
| ωB |
两行星相距最近时,两行星应该在同一半径方向上.
所以当A比B多转一圈时两行星再次相距最近,列出等式:
(
| 2π |
| T1 |
| 2π |
| T2 |
t=
| T1T2 |
| T2-T1 |
C、D、两行星相距最远时,两行星应该在同一直径上.
所以当A比B多转半圈时两行星相距最远,列出等式:
(
| 2π |
| T1 |
| 2π |
| T2 |
t′=
| T1T2 |
| 2(T2-T1) |
故选:BD.

练习册系列答案
相关题目