题目内容
在如图所示的水平导轨上(摩擦、电阻忽略不计),有竖直向下的匀强磁场,磁感强度B,导轨左端的间距为L1=4l0,右端间距为l2=l0。今在导轨上放置AC、DE两根导体棒,质量分别为m1=2m0,m2=m0,电阻R1=4R0,R2=R0。若AC棒以初速度v0向右运动,求AC棒运动的过程中产生的总焦耳热QAC,以及通过它们的总电量q。




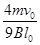
【错解分析】AC棒在磁场力的作用下,做变速运动。运动过程复杂,应从功能关系的角度来分析。由于没有摩擦,最后稳定的状态应为两棒做匀速运动。根据动量守恒定律m1v0 = (m1+m2)v′

整个回路产生的焦耳热

因为R1=4R0,R2=R0。所以AC棒在运动过程中产生的焦耳热

对AC棒应用动量定理 - Bll·Δt = m1v′1 - m1v0

错解原因:AC棒在磁场力的作用下做变速运动,最后达到运动稳定,两棒都做匀速运动的分析是正确的。但是以此类推认为两棒的运动速度相同是错误的。如果两棒的速度相同则回路中还有磁通量的变化,还会存在感应电动势,感应电流还会受到安培力的作用,AC,DE不可能做匀速运动。
【正解】由于棒l1向右运动,回路中产生电流,ll受安培力的作用后减速,l2受安培力加速使回路中的电流逐渐减小。只需v1,v2满足一定关系,就有可能使回路的
 ,及电动势为零,此后不再受安培力的作用。
,及电动势为零,此后不再受安培力的作用。两棒做匀速运动。
两棒匀速运动时,I=0,即回路的总电动势为零。所以有
Bllv1=Bl2v2
 时,回路电流为零,此后两棒匀速运动,对AC棒应用动量定理
时,回路电流为零,此后两棒匀速运动,对AC棒应用动量定理
再对DE棒应用动量定理 Bl2Δt = m2v2
解得:


【点评】以前我们做过类似的题。那道题中的平行轨道间距都是一样的。有一些同学不假思索,把那道题的结论照搬到本题中来,犯了生搬硬套的错误。差异就是矛盾。两道题的差别就在平行导轨的宽度不一样上。如何分析它们之间的差别呢?还是要从基本原理出发。平行轨道间距一样的情况两根导体棒的速度相等,才能使回路中的磁通量的变化为零。本题中如果两根导轨的速度一样,由于平行导轨的宽度不同导致磁通量的变化不为零,仍然会有感应电流产生,两根导体棒还会受到安培力的作用,其中的一根继续减速,另一根继续加速,直到回路中的磁通量的变化为零,才使得两根导体棒做匀速运动。抓住了两道题的差异之所在,问题就会迎刃而解。

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目




 和物块B的运动时间?
和物块B的运动时间?





 ,载有质量为50
,载有质量为50